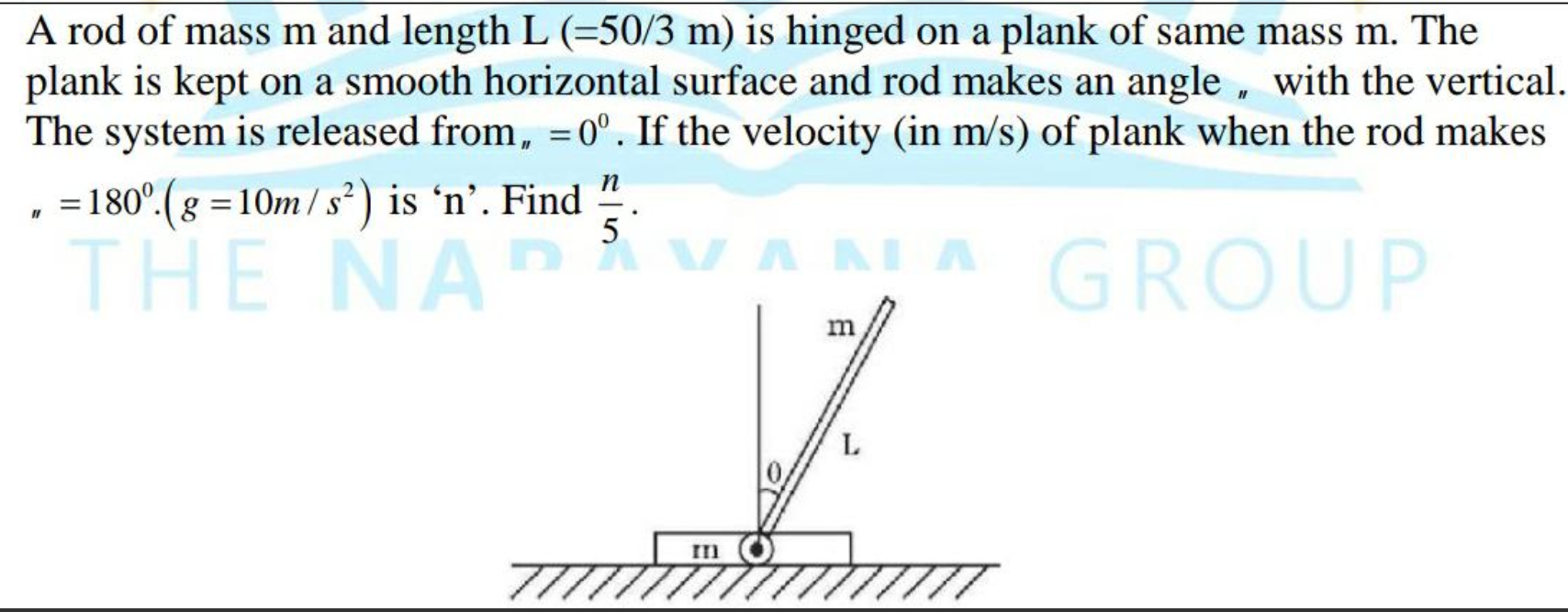
A rod of mass m and length L (=50/3 m) is hinged on a plank of the same mass m. The plank is kept on a smooth horizontal surface, and the rod makes an angle θ with the vertical. Th... A rod of mass m and length L (=50/3 m) is hinged on a plank of the same mass m. The plank is kept on a smooth horizontal surface, and the rod makes an angle θ with the vertical. The system is released from θ = 0°. If the velocity (in m/s) of the plank when the rod makes θ = 180° (g = 10 m/s²) is ‘n’, find n/5. Read more

Steps to Solve

1. Identify the Initial and Final Configurations

The rod is initially vertical ($\theta = 0^\circ$) and then released to make an angle $\theta = 180^\circ$. The conservation of energy principle will be used here.

2. Calculate the Initial Potential Energy

The initial potential energy (PE_initial) of the rod, when it is vertical, can be expressed as:

$$ \text{PE}_{\text{initial}} = mgh $$

Where $h$ is the center of mass of the rod at the vertical position which is $\frac{L}{2}$. Thus: $$ \text{PE}_{\text{initial}} = mg\left(\frac{L}{2}\right) $$

3. Calculate the Final Potential Energy

At the angle of $\theta = 180^\circ$, the rod is completely horizontal, and the height of the center of mass becomes $h = 0$. Thus: $$ \text{PE}_{\text{final}} = 0 $$

4. Use Conservation of Mechanical Energy

According to the conservation of energy:

$$ \text{PE}{\text{initial}} = \text{KE}{\text{final}} $$

The final kinetic energy (KE) of the plank when the rod makes an angle $\theta$ is given by: $$ \text{KE} = \frac{1}{2} mv^2 + \frac{1}{2} I\omega^2 $$ Where $I$ is the moment of inertia of the rod, which is $I = \frac{1}{3}mL^2$, and $\omega$ is the angular velocity, given by $v = \omega L$ for the end of the rod.

5. Substituting into the Energy Equation

Set the initial potential energy equal to the sum of the kinetic energies: $$ mg\left(\frac{L}{2}\right) = \frac{1}{2} mv^2 + \frac{1}{2} \left(\frac{1}{3} m L^2\right \frac{v^2}{L^2} $$

6. Solve for Velocity $v$ of the Plank

Combine and solve for $v$: $$ mg\left(\frac{L}{2}\right) = \frac{1}{2} mv^2 + \frac{1}{6} mv^2 $$ This simplifies to: $$ mg\left(\frac{L}{2}\right) = \frac{2}{3} mv^2 $$ Dividing by $m$ (assuming $m\neq0$) gives: $$ g\left(\frac{L}{2}\right) = \frac{2}{3} v^2 $$ Now, solve for $v$: $$ v^2 = \frac{3gL}{4} \implies v = \sqrt{\frac{3gL}{4}} $$

7. Insert the Given Values

Given $g = 10 m/s^2$ and $L = \frac{50}{3} m$: $$ v = \sqrt{\frac{3 \cdot 10 \cdot \left(\frac{50}{3}\right)}{4}} = \sqrt{\frac{1500}{4}} = \sqrt{375} = 5\sqrt{15} \text{ m/s} $$