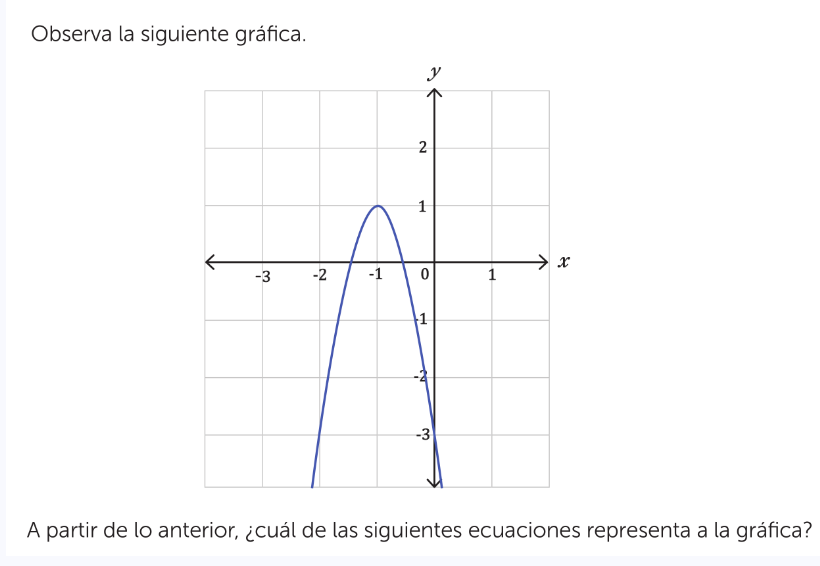
A partir de lo anterior, ¿cuál de las siguientes ecuaciones representa a la gráfica?
Understand the Problem
La pregunta está pidiendo identificar cuál de las ecuaciones dadas representa la gráfica mostrada. Se está proporcionando una gráfica y se requiere que se relacione con las ecuaciones posibles.
Answer
La ecuación es $y = ax^2 + bx - 3$ con $a > 0$.
Answer for screen readers
La ecuación que representa la gráfica es $y = ax^2 + bx - 3$ con $a > 0$.
Steps to Solve
-
Analizar la gráfica La gráfica muestra una parábola que tiene un punto mínimo. Observamos que la parábola tiene su vértice en el punto (0, -3) y cruza el eje y en -3. Esto sugiere que la ecuación de la parábola podría ser del tipo $y = ax^2 + bx + c$.
-
Identificar el vértice El vértice de la parábola, que es el punto más bajo, se encuentra en (0, -3). Por lo tanto, $c = -3$.
-
Determinar el coeficiente a Como la parábola se abre hacia arriba, el coeficiente $a$ debe ser positivo. También, observamos que la parábola pasa por otros puntos, como (-1, -2) y (1, -2). Usaremos estos puntos para encontrar el valor de $a$.
-
Usar un punto para encontrar a Sustituyamos el punto (-1, -2) en la ecuación: $$ -2 = a(-1)^2 + b(-1) - 3 $$ Resolvamos para $a$ y $b$ considerando que sabemos que $c = -3$.
-
Investigación de las opciones Con el valor de $a$, veremos si alguna de las ecuaciones propuestas se ajusta a los datos obtenidos (punto mínimo en (0, -3) y apertura hacia arriba).
La ecuación que representa la gráfica es $y = ax^2 + bx - 3$ con $a > 0$.
More Information
Las parábolas son gráficas de funciones cuadráticas, y su forma general es $y = ax^2 + bx + c$. El vértice y la dirección de apertura son características clave para determinar su ecuación.
Tips
- No identificar correctamente el signo del coeficiente $a$. Siempre revisa si la parábola se abre hacia arriba o hacia abajo.
- Olvidar sustituir correctamente los valores en la ecuación. Asegúrate de operar cuidadosamente.
AI-generated content may contain errors. Please verify critical information