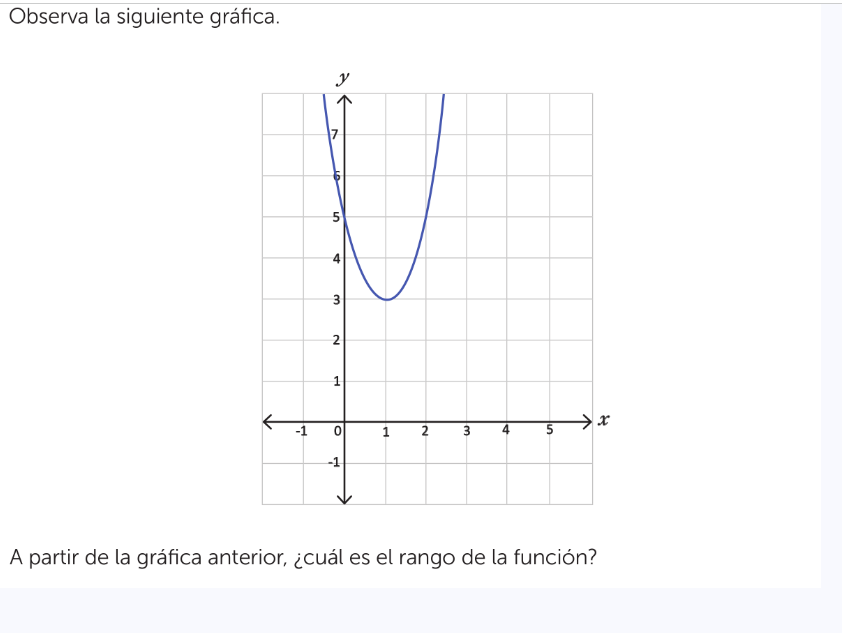
A partir de la gráfica anterior, ¿cuál es el rango de la función?
Understand the Problem
La pregunta está pidiendo determinar el rango de una función a partir de la gráfica proporcionada. Se requiere observar la gráfica y deducir los valores posibles de y.
Answer
El rango de la función es $[3, \infty)$.
Answer for screen readers
El rango de la función es $[3, \infty)$.
Steps to Solve
-
Identificación de la gráfica Observamos que la gráfica es una parábola que se abre hacia arriba, lo que sugiere que el valor mínimo de la función es crucial para determinar el rango.
-
Determinación del valor mínimo La parábola alcanza su punto más bajo en $y = 3$. Por lo tanto, este valor es el mínimo en el rango de la función.
-
Establecimiento del rango Dado que la parábola se abre hacia arriba, los valores de $y$ pueden ser iguales o superiores a 3. Así, el rango se expresa como $[3, \infty)$.
El rango de la función es $[3, \infty)$.
More Information
El rango de una función cuadrática depende de la dirección en que abre la parábola y su valor mínimo. En este caso, la parábola abre hacia arriba, por lo que el rango se extiende hasta infinito desde su mínimo.
Tips
- Confundir el mínimo con el máximo: Asegúrate de identificar correctamente si la parábola abre hacia arriba o hacia abajo antes de determinar el rango.
- Olvidar incluir el rango en forma de intervalo: Los estudiantes a veces solo mencionan el valor mínimo sin expresarlo como un intervalo.
AI-generated content may contain errors. Please verify critical information