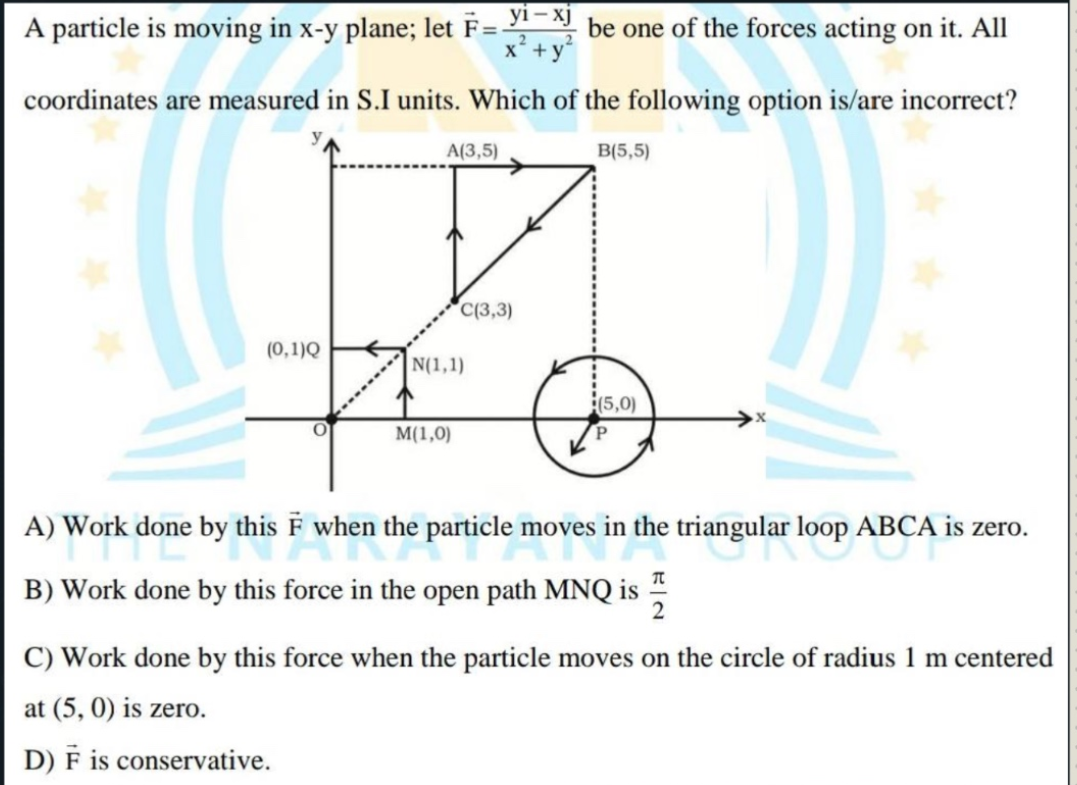
A particle is moving in x-y plane; let F = (y i - x j)/(x^2 + y^2) be one of the forces acting on it. All coordinates are measured in S.I. units. Which of the following options is/... A particle is moving in x-y plane; let F = (y i - x j)/(x^2 + y^2) be one of the forces acting on it. All coordinates are measured in S.I. units. Which of the following options is/are incorrect? A) Work done by this F when the particle moves in the triangular loop ABCA is zero. B) Work done by this force in the open path MNQ is π/2. C) Work done by this force when the particle moves on the circle of radius 1 m centered at (5,0) is zero. D) F is conservative.
Understand the Problem
The question is asking about the work done by a given force in different paths taken by a particle in a 2D plane. It asks which of the provided statements about the work done is incorrect. The statements involve specific paths and conditions related to physics principles such as work done by forces and conservative forces.
Answer
C) Work done by this force when the particle moves on the circle of radius 1 m centered at (5, 0) is zero.
Answer for screen readers
The incorrect statement is C) Work done by this force when the particle moves on the circle of radius 1 m centered at (5, 0) is zero.
Steps to Solve
- Understand the Force Expression
The force is given as
$$ \vec{F} = \frac{y\hat{i} - x\hat{j}}{x^2 + y^2} $$
This indicates that the force depends on the position in the 2D plane.
- Check for Conservative Forces
A force is conservative if the work done is independent of the path taken. To check this, we can determine if the line integral around any closed path equals zero.
- Evaluate Work Done in Path ABCD
Calculate the work done around the triangular path ABC to confirm if it is zero. The vertices are:
- A(3,5)
- B(5,5)
- C(3,3)
Calculate the work done along each segment:
- From A to B
- From B to C
- From C to A
- Evaluate Work Done in Path MNQ
Calculate the work done along the open path MNQ, where M(1,0), N(1,1), and Q(0,1). Find the path and compute the work done.
- Evaluate Work Done on Circle Path
For a circular path around the origin with center at (5,0), the parameterization can be used. Depending on the force's nature, determine if the work done is indeed zero.
- Compare Results
Review the calculated work for each path described and compare them with the statements given to identify any incorrect options.
The incorrect statement is C) Work done by this force when the particle moves on the circle of radius 1 m centered at (5, 0) is zero.
More Information
Statement C is incorrect because forces that depend on the position do not guarantee zero work on certain paths, especially when there is path dependence.
Tips
- Assuming that all paths will yield the same work done without checking if the force is conservative.
- Incorrectly calculating the integral for work done along the paths.
AI-generated content may contain errors. Please verify critical information