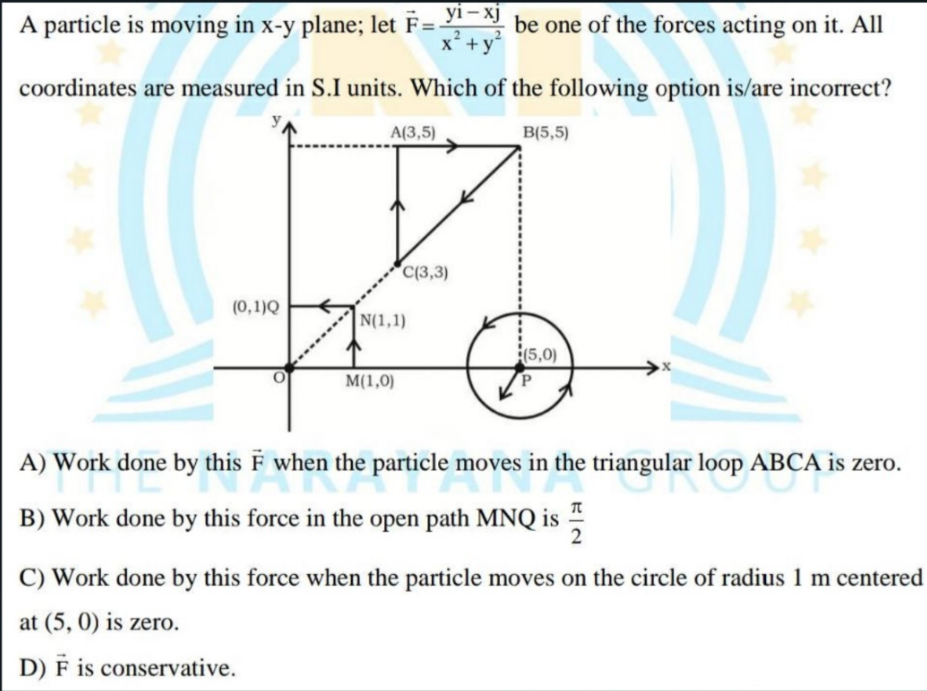
A particle is moving in x-y plane; let F = (y i - x j) / (x^2 + y^2) be one of the forces acting on it. All coordinates are measured in S.I units. Which of the following option is/... A particle is moving in x-y plane; let F = (y i - x j) / (x^2 + y^2) be one of the forces acting on it. All coordinates are measured in S.I units. Which of the following option is/are incorrect? A) Work done by this F when the particle moves in the triangular loop ABCA is zero. B) Work done by this force in the open path MNQ is π/2. C) Work done by this force when the particle moves on the circle of radius 1 m centered at (5, 0) is zero. D) F is conservative.
Understand the Problem
The question involves a particle moving in the x-y plane under a force defined by a specific equation. It asks which of the given statements about work done by the force in different scenarios is incorrect. This requires an understanding of physics concepts related to work and forces, particularly in the context of conservative forces.
Answer
Incorrect option: B) Work done by this force in the open path MNQ is $\frac{\pi}{2}$.
Answer for screen readers
The incorrect option is B) Work done by this force in the open path MNQ is $\frac{\pi}{2}$.
Steps to Solve
- Identify the Nature of the Force
The given force is $\mathbf{F} = \left( \frac{y}{x^2 + y^2}, -\frac{x}{x^2 + y^2} \right)$. This force is derived from a potential function indicating that it is a conservative force.
- Evaluate Work Done on Closed Path ABCDA
For conservative forces, the work done on a closed path (like triangle ABC) is always zero. Thus, the work done in moving around the triangular loop ABC is zero.
- Calculate Work Done Along Path MNQ
To evaluate the work done on the path MNQ, integrate the force along the path. This requires calculating the appropriate line integral. However, the work done would relate to the potential difference associated with movement from M to N to Q.
- Evaluate Work Done in Circular Path at (5,0)
For a circular path with a radius of 1 m centered at P(5,0), if it doesn't enclose any singularity of the force function, the work done is expected to be zero, as in any closed path for conservative forces.
- Determine the Conservativeness of the Force
Since the force has a potential function and the work done in a closed path is zero, this force is conservative.
The incorrect option is B) Work done by this force in the open path MNQ is $\frac{\pi}{2}$.
More Information
The force given is a conservative force. For conservative forces, the work done in a closed loop is zero. However, if you calculate the work for open paths, it's different but doesn't lead to simple expressions like the provided options suggest.
Tips
- Failing to recognize that the work done in a closed loop for conservative forces is always zero can lead to incorrect conclusions about paths like ABCDA.
- Miscalculating the line integral for open paths and confusing them with conservative work can result in incorrect results, especially in parts like MNQ.
AI-generated content may contain errors. Please verify critical information