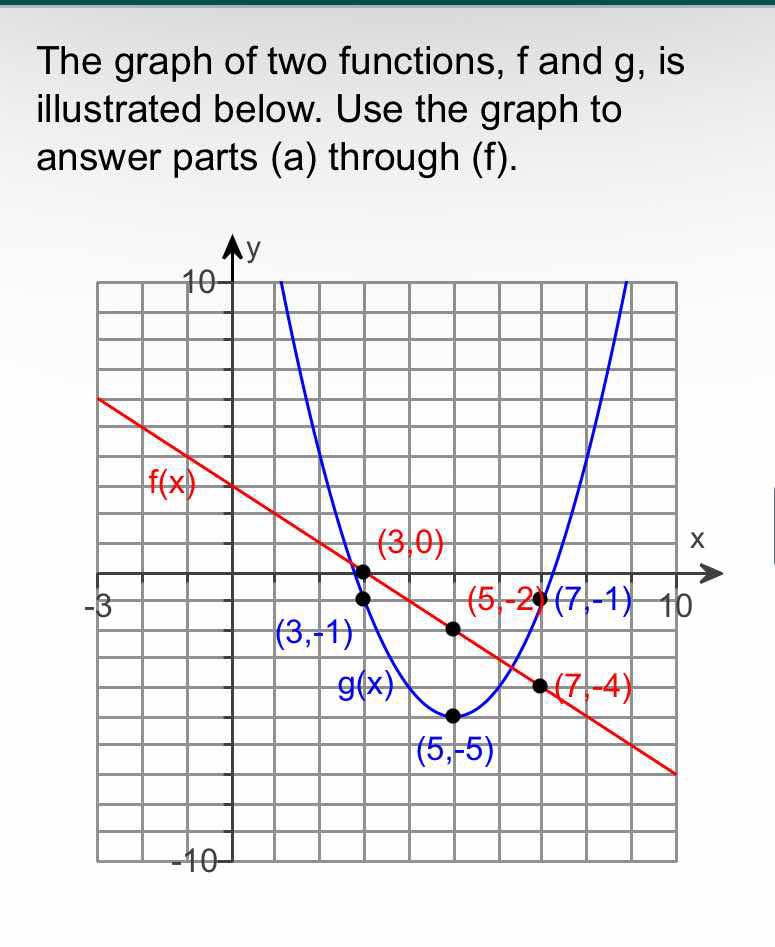
The graph of two functions, f and g, is illustrated below. Use the graph to answer parts (a) through (f).
Understand the Problem
The question involves analyzing the given graph of two functions, f and g, and requires answering parts (a) through (f) based on the visual information provided. This likely involves interpreting values, intersections, or specific points on the graph.
Answer
Key intersection point: \( (5, -2) \) for \( f(x) = g(x) \).
Answer for screen readers
The answers to the parts (a) through (f) would vary based on the specific questions within each part, which aren't provided.
Key values include:
- Intersection at ( (5, -2) )
- Vertex of ( g(x) ) at ( (5, 5) )
- Points ( (3, 0) ) for ( f(x) ) and ( (3, 1) ) for ( g(x) )
Steps to Solve
-
Identify Key Points on the Graph
From the graph, observe the coordinates of crucial intersection points and vertex points for the functions ( f(x) ) and ( g(x) ). Notable points include:
- Intersection of ( f ) and ( g ) at ( (5, -2) )
- The vertex of ( g(x) ) at ( (5, 5) )
- Other points: ( f(0) = -3 ), ( g(3) = 1 ), ( f(3) = 0 ), ( g(7) = -4 )
-
Analyze Function Behavior
Examine the overall behavior of both functions:
- ( f(x) ) appears to be a linear function with a negative slope.
- ( g(x) ) is a quadratic function with its vertex indicating a minimum point.
-
Determine Function Values at Specific Points
Evaluate ( f(x) ) and ( g(x) ) at specific x-values:
- For ( f(3) ) and ( g(3) ), ( f(3) = 0 ) and ( g(3) = 1 ).
- For ( g(5) ), observe that ( g(5) = 5 ).
- For ( g(7) ), ( g(7) = -4 ).
-
Finding Intersections
The intersection points of ( f(x) ) and ( g(x) ) occur where ( f(x) = g(x) ). From the graph, we see one intersection at ( (5, -2) ).
-
Discuss Range and Domain
Determine the domain and range for both functions based on their visual representation.
- The domain of ( f(x) ) is all real numbers, while the range is ( y < 0 ) (falls).
- The domain of ( g(x) ) is also all real numbers, but the range is ( y \geq -4 ) (since it is a parabola opening upwards).
-
Answer Specific Questions (Parts a-f)
Identify pieces of information needed for the problem parts, using the analyzed graph data to make accurate assertions about values, intersections, and outputs related to ( f ) and ( g ).
The answers to the parts (a) through (f) would vary based on the specific questions within each part, which aren't provided.
Key values include:
- Intersection at ( (5, -2) )
- Vertex of ( g(x) ) at ( (5, 5) )
- Points ( (3, 0) ) for ( f(x) ) and ( (3, 1) ) for ( g(x) )
More Information
The graph illustrates the interaction between a linear function and a quadratic function, showing key points of intersection and the behavior of the functions over the x-axis.
Tips
- Confusing the intersection points with the vertex of a function.
- Misinterpreting the range and domain of the functions based solely on visual inspection without calculation.
AI-generated content may contain errors. Please verify critical information