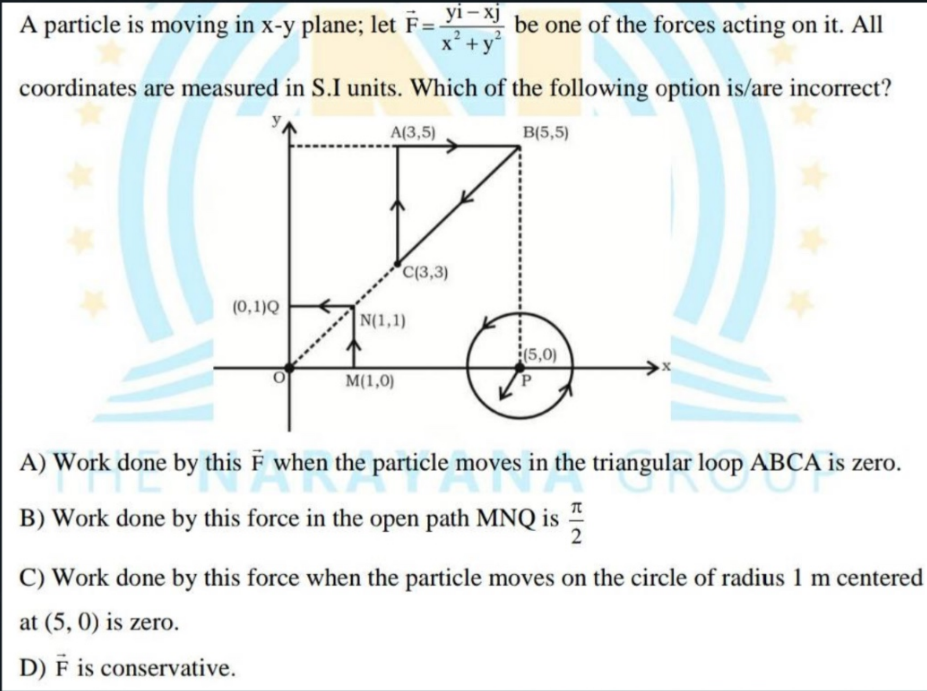
A particle is moving in x-y plane; let F = (y i - x j) / (x^2 + y^2) be one of the forces acting on it. All coordinates are measured in S.I. units. Which of the following options i... A particle is moving in x-y plane; let F = (y i - x j) / (x^2 + y^2) be one of the forces acting on it. All coordinates are measured in S.I. units. Which of the following options is/are incorrect? A) Work done by this F when the particle moves in the triangular loop ABCA is zero. B) Work done by this force in the open path MNQ is π/2. C) Work done by this force when the particle moves on the circle of radius 1 m centered at (5, 0) is zero. D) F is conservative. Read more

Steps to Solve

1. Identifying the Force The force acting on the particle is given by (\mathbf{F} = \frac{y \mathbf{i} - x \mathbf{j}}{x^2 + y^2}).

2. Checking if the Force is Conservative To check if the vector field is conservative, we need to see if the curl of (\mathbf{F}) is zero. If (\nabla \times \mathbf{F} = 0), then the force is conservative. Calculate the components:

• (\frac{\partial F_y}{\partial x}) and (\frac{\partial F_x}{\partial y})

3. Calculating Work Done in a Closed Path (ABCA) For a conservative force, the work done in a closed path is zero. We can analyze the triangular path ABC. Thus, if (\mathbf{F}) is conservative, work along path ABCA will be zero.

4. Calculating Work Done Along Path MNQ The work done by (\mathbf{F}) along path MNQ can be calculated through line integration: $$ W = \int_C \mathbf{F} \cdot d\mathbf{r} $$

5. Calculating Work Done Along the Circle For the circle of radius 1 m centered at (5, 0), we evaluate the work done similarly using the line integral. Points on the circle need to be parameterized.

6. Comparing Statements Now we will verify each statement:

• A) Work in triangle ABC being zero (if conservative).
• B) Given ( W = \frac{\pi}{2} ).
• C) Circle center work being zero (as expected for conservative).
• D) Review if (\mathbf{F}) is conservative.