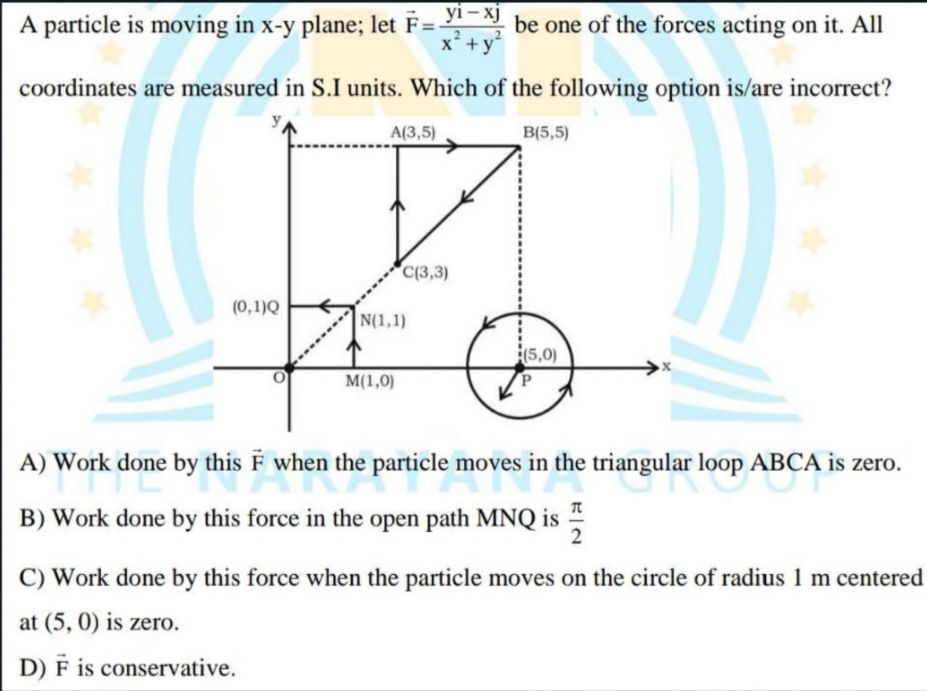
A particle is moving in x-y plane; let F be one of the forces acting on it. All coordinates are measured in S.I units. Which of the following option is/are incorrect? A) Work done... A particle is moving in x-y plane; let F be one of the forces acting on it. All coordinates are measured in S.I units. Which of the following option is/are incorrect? A) Work done by this F when the particle moves in the triangular loop ABCA is zero. B) Work done by this force in the open path MNQ is π/2. C) Work done by this force when the particle moves on the circle of radius 1 m centered at (5, 0) is zero. D) F is conservative. Read more

Steps to Solve

1. Calculate Work Done in Triangular Loop ABCA

To determine if the work done by the force $\vec{F}$ when the particle moves in the triangular loop ABCA is zero, we use the concept that if the force is conservative, the work done along a closed loop is zero. We'll need to check whether the force $\vec{F} = \frac{y \hat{i} - x \hat{j}}{x^2 + y^2}$ is conservative by checking if it has a scalar potential.

2. Check for Conservativeness of the Force

A force is conservative if its curl is zero. The curl of a two-dimensional vector field $\vec{F}(x,y) = P(x,y) \hat{i} + Q(x,y) \hat{j}$ is defined as:

$$ \text{curl} , \vec{F} = \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} $$

For $\vec{F}(x,y) = \left( \frac{y}{x^2 + y^2}, -\frac{x}{x^2 + y^2} \right)$:

• Set ( P = \frac{y}{x^2 + y^2} ) and ( Q = -\frac{x}{x^2 + y^2} )

3. Calculate Partial Derivatives

Now, calculate the derivative:

• ( \frac{\partial Q}{\partial x} = \frac{\partial}{\partial x} \left(-\frac{x}{x^2 + y^2}\right) = -\frac{(x^2 + y^2) - 2x^2}{(x^2 + y^2)^2} = -\frac{y^2 - x^2}{(x^2 + y^2)^2} )

• ( \frac{\partial P}{\partial y} = \frac{\partial}{\partial y} \left(\frac{y}{x^2 + y^2}\right) = \frac{(x^2 + y^2) - 2y^2}{(x^2 + y^2)^2} = \frac{x^2 - y^2}{(x^2 + y^2)^2} )

Now substituting these derivatives into the curl formula:

$$ \text{curl} , \vec{F} = -\frac{y^2 - x^2}{(x^2 + y^2)^2} - \frac{x^2 - y^2}{(x^2 + y^2)^2} = 0 $$

Therefore, $\vec{F}$ is conservative.

4. Work Done Along Path MNQ Calculation

For the path MNQ, the work done can be calculated using line integrals, but we already established that the force is conservative, implying the work done is path independent. If we know the starting and ending points, the work done would be zero for any closed loop.

• Thus, the work done by the force along path MNQ, where the beginning and end points are the same, is zero, and the statement claiming it to be $\frac{\pi}{2}$ is incorrect.

5. Work Done on Circle of Radius 1 m

Next, check the circular path centered at (5, 0) with radius 1 m. For a conservative force, the work done depends only on the initial and final positions. Since this path does not return to its start, we cannot state the work is zero on this path.

6. Check If Force is Conservative

Finally, based on the findings in step 3, the force $\vec{F}$ being conservative implies that the work done is independent of the path taken.