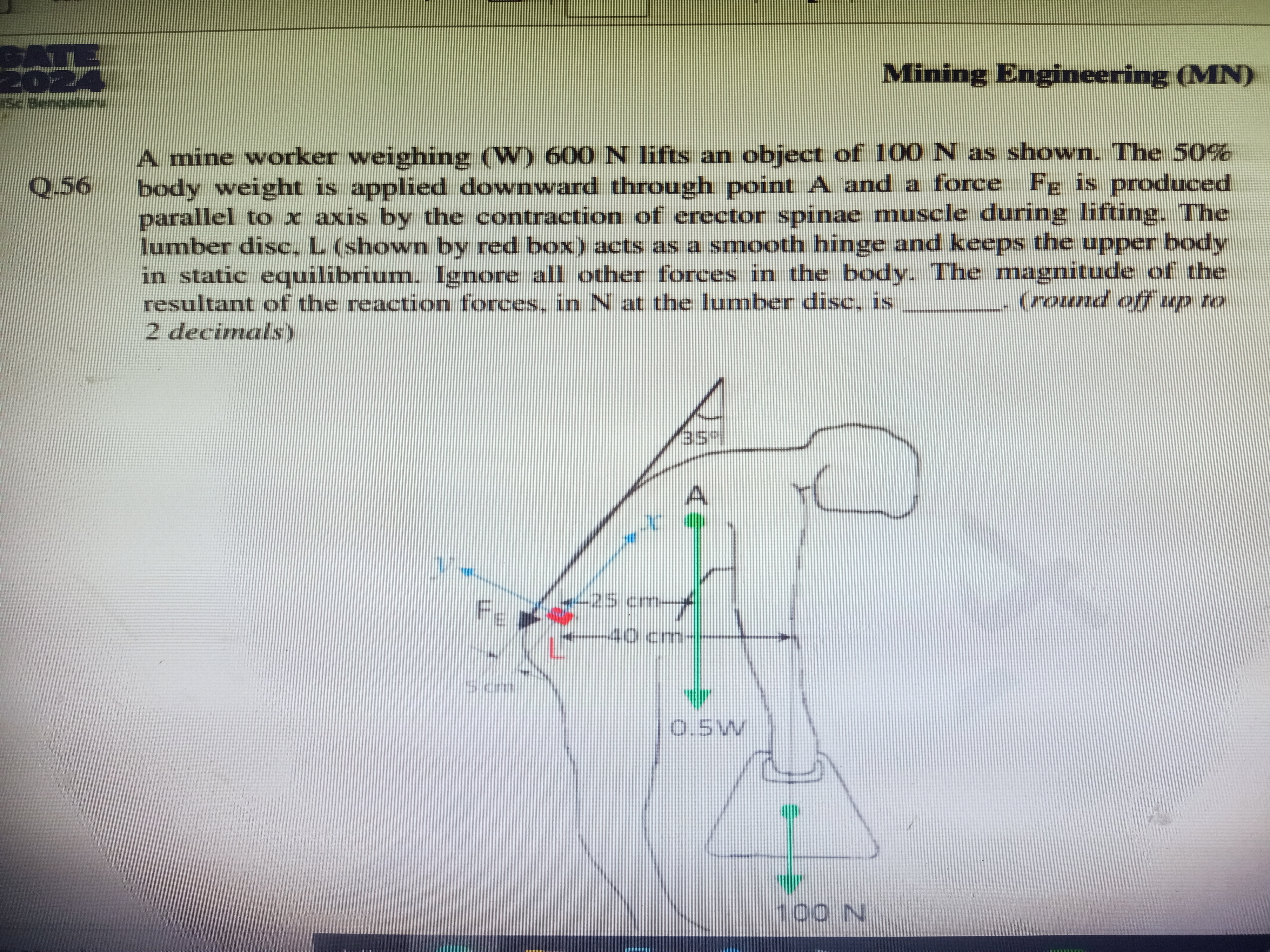
A mine worker weighing 600 N lifts an object of 100 N. The 50% body weight is applied downward through point A, and a force F_E is produced parallel to the x-axis. The lumber disc... A mine worker weighing 600 N lifts an object of 100 N. The 50% body weight is applied downward through point A, and a force F_E is produced parallel to the x-axis. The lumber disc acts as a smooth hinge and keeps the upper body in static equilibrium. Ignore all other forces in the body. Calculate the magnitude of the resultant of the reaction forces at the lumber disc, rounding off to 2 decimals. Read more

Steps to Solve

1. Determine Forces Acting on the Body

   • The weight of the worker ($W = 600 , \text{N}$) is applied downward through point A at 50%, so the force is: $$ F_W = 0.5 \times W = 0.5 \times 600 = 300 , \text{N} $$

2. Identify the Forces Involved

   • The object being lifted exerts a force of: $$ F_{obj} = 100 , \text{N} $$

3. Calculate the Resultant Moment about Point L

   • The moments about point L need to consider both the downward forces and the lever arms. The lever arm for the worker's weight ($300 , \text{N}$) is 0.40 m (total distance) and for the object is 0.25 m: [ \text{Moment}W = 300 , \text{N} \times 0.40 , \text{m} = 120 , \text{Nm} \quad \text{(counter-clockwise)} ] [ \text{Moment}{obj} = 100 , \text{N} \times 0.25 , \text{m} = 25 , \text{Nm} \quad \text{(clockwise)} ]

4. Set Up the Equation for Static Equilibrium

   • Since the system is in equilibrium, the total moments about point L must balance: $$ \text{Moment}W = \text{Moment}{obj} + \text{Moment}_{F_E} $$
   • Let $M_{F_E}$ be the moment due to the erector spinae muscle: $$ M_{F_E} = 120 - 25 = 95 , \text{Nm} $$

5. Calculate the Force $F_E$

   • The moment due to the muscle force $F_E$ acting 0.05 m from point L is: $$ M_{F_E} = F_E \times 0.05 $$
   • Thus: $$ 95 = F_E \times 0.05 $$ $$ F_E = \frac{95}{0.05} = 1900 , \text{N} $$

6. Find the Resultant Reaction Forces at the Lumber Disc

   • Summing all forces in the vertical direction gives: $$ R_y + F_E - F_W - F_{obj} = 0 $$
   • Where $R_y$ is the reaction force at the lumber disc: $$ R_y = F_W + F_{obj} - F_E $$ $$ R_y = 300 + 100 - 1900 $$ $$ R_y = 400 - 1900 = -1500 , \text{N} $$

7. Magnitude of Reaction Force

   • The reaction force magnitude is considered a positive value: $$ |R_y| = 1500 , \text{N} $$