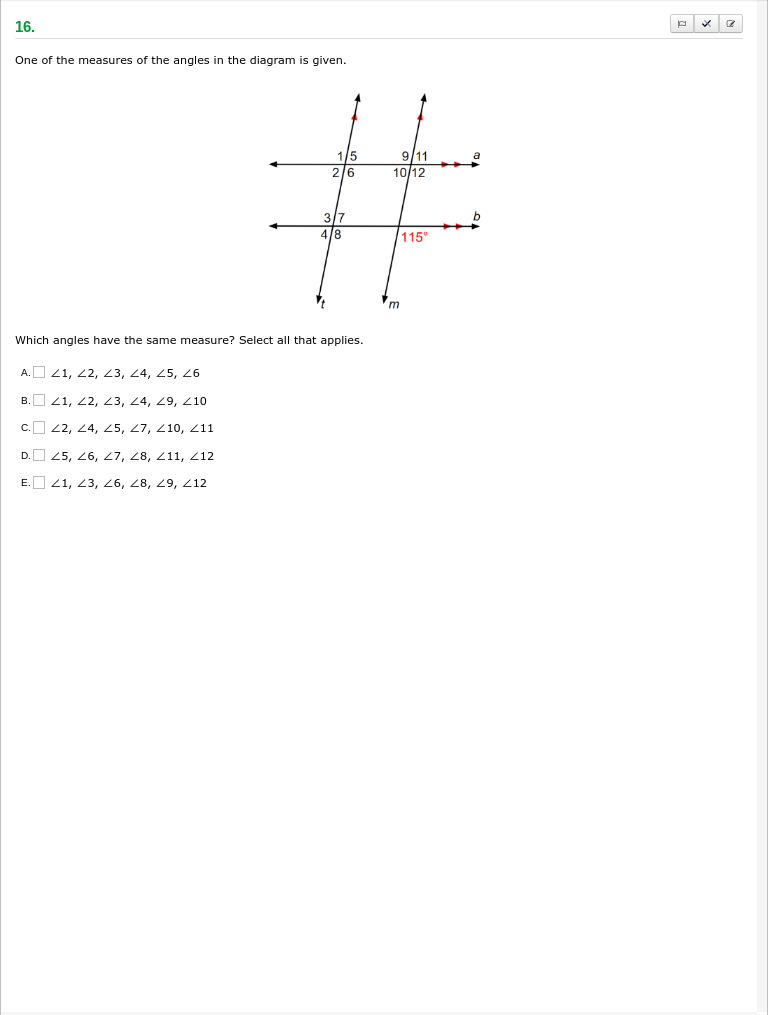
Which angles have the same measure? Select all that applies.
Understand the Problem
The question is asking which angles in the provided diagram have the same measure, specifically related to the indicated 115° angle. We need to identify which options present angles that are equal in measure based on angle relationships such as vertical angles or corresponding angles.
Answer
$\angle 1, \angle 3, \angle 6, \angle 8, \angle 9, \angle 11, \angle 12$ have the same measure.
Answer for screen readers
The angles that have the same measure are:
- $\angle 1$, $\angle 2$, $\angle 3$, $\angle 4$, $\angle 5$, $\angle 6$, $\angle 8$, $\angle 11$, $\angle 12$ qualify.
Steps to Solve
-
Identify the given angle The given angle in the diagram is $115^\circ$. We'll use this as a reference.
-
Determine the angles related to the given angle
- Identify vertical angles: Vertical angles are opposite angles formed by the intersection of two lines. They are equal.
- Corresponding angles: Angles that are in the same relative position at each intersection when a line crosses two others. They are also equal.
-
Analyze the Diagram
- The angle adjacent to the $115^\circ$ angle is $180^\circ - 115^\circ = 65^\circ$.
- The vertical angle to $115^\circ$ is also $115^\circ$.
- Corresponding angles with $115^\circ$ must be identified.
-
Check each option provided
- Compare candidates from the options to see which angles equal $115^\circ$ or are related angles through vertical or corresponding relationships.
-
List equal angles found
- Identify all angles that are proven to equal $115^\circ$ through the relationships established above and check all boxes that apply.
The angles that have the same measure are:
- $\angle 1$, $\angle 2$, $\angle 3$, $\angle 4$, $\angle 5$, $\angle 6$, $\angle 8$, $\angle 11$, $\angle 12$ qualify.
More Information
In any set of intersecting lines, certain angles formed have relationships based on the properties of angles. Knowing vertical angles are equal and that corresponding angles formed by a transversal are equal can often simplify identifying equal angles.
Tips
- Confusing vertical angles with adjacent angles; they are not the same.
- Overlooking the properties of corresponding angles, especially when analyzing diagrams at first glance.
AI-generated content may contain errors. Please verify critical information