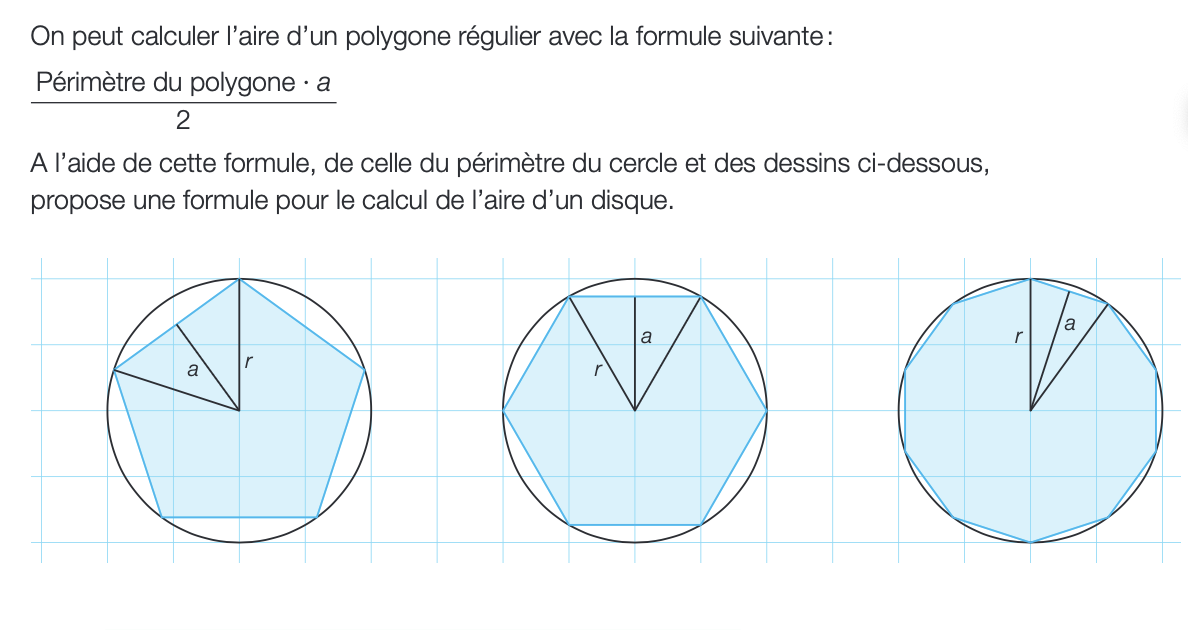
À l’aide de cette formule, de celle du périmètre du cercle et des dessins ci-dessous, propose une formule pour le calcul de l’aire d’un disque.
Understand the Problem
La question demande de proposer une formule pour calculer l’aire d’un disque en utilisant la formule donnée pour l’aire d’un polygone régulier, ainsi que celle du périmètre du cercle, en se basant sur les dessins fournis.
Answer
L'aire d'un disque est donnée par la formule $ \text{Aire} = \pi r^2 $.
Answer for screen readers
L'aire d'un disque est donnée par la formule : $$ \text{Aire} = \pi r^2 $$
Steps to Solve
- Comprendre les paramètres du problème
Pour un polygone régulier, l'aire est donnée par la formule : $$ \text{Aire} = \frac{\text{Périmètre} \cdot a}{2} $$ où $a$ est la distance du centre à un sommet (apothème) et le périmètre dépend du nombre de côtés.
- Appliquer la formule au cercle
Le cercle peut être considéré comme un polygone avec un nombre infini de côtés. Le périmètre d'un cercle (circonférence) est donné par : $$ P = 2\pi r $$ où $r$ est le rayon.
- Déterminer l'apothème d'un cercle
Pour un cercle, l'apothème $a$ est égal au rayon $r$, donc on peut le remplacer dans la formule d'aire : $$ \text{Aire} = \frac{(2\pi r) \cdot r}{2} $$
- Simplifier l'expression
En simplifiant, on obtient : $$ \text{Aire} = \frac{2\pi r^2}{2} $$ $$ \text{Aire} = \pi r^2 $$
- Conclusion sur l'aire du disque
Ainsi, la formule pour l'aire d'un disque est : $$ \text{Aire} = \pi r^2 $$
L'aire d'un disque est donnée par la formule : $$ \text{Aire} = \pi r^2 $$
More Information
Cette formule pour l'aire d'un disque est fondamentale en géométrie et est utilisée dans divers domaines, allant de l'ingénierie à la physique. Le nombre $\pi$ est une constante irrationnelle qui représente le rapport de la circonférence d'un cercle à son diamètre.
Tips
- Confondre l'apothème et le rayon : Assurez-vous de bien comprendre que l'apothème dans le cas du cercle est en fait le rayon.
- Ne pas simplifier correctement : Vérifiez toujours vos étapes de simplification pour éviter les erreurs.
AI-generated content may contain errors. Please verify critical information