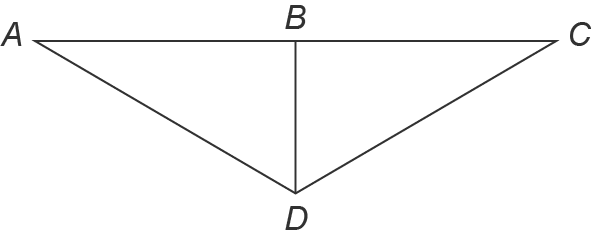
(a) Jeremy says that two triangles are congruent by the SAS congruence postulate. Do you agree or disagree? Explain. (b) Suppose it is also known that triangle ABC is isosceles. Wh... (a) Jeremy says that two triangles are congruent by the SAS congruence postulate. Do you agree or disagree? Explain. (b) Suppose it is also known that triangle ABC is isosceles. Which postulate or theorem can be used to prove that triangle ABD is congruent to triangle CBD?
Understand the Problem
The question is asking for an evaluation of Jeremy's claim regarding the SAS congruence postulate and a related question on identifying a postulate or theorem to prove another statement involving the triangles shown in the diagram.
Answer
The triangles $ABD$ and $BDC$ are congruent by the SAS postulate.
Answer for screen readers
The triangles $ABD$ and $BDC$ are congruent by the SAS congruence postulate.
Steps to Solve
- Identify the triangles involved
In the diagram, there are two triangles: triangle $ABD$ and triangle $BDC$. We need to evaluate whether these triangles are congruent using the SAS (Side-Angle-Side) congruence postulate.
- Analyze the triangle sides
We observe that:
- Side $AB$ is equal to side $BC$ (both are parts of the same line).
- Side $AD$ is vertical and is a right angle at point $B$ (90 degrees).
- Check the included angle
The included angle between sides $AB$ and $AD$ is $\angle ABD$. Since side $AD$ is vertical and it meets side $AB$ at point $B$, it is a right angle.
- Evaluate triangle congruence using SAS
We now use the SAS postulate:
- We have side $AB$ equal to side $BC$.
- The angle $\angle ABD$ is 90 degrees.
- Lastly, side $AD$ is common to both triangles.
Thus, by SAS, we conclude that triangles $ABD$ and $BDC$ are congruent.
The triangles $ABD$ and $BDC$ are congruent by the SAS congruence postulate.
More Information
The SAS postulate states that if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the two triangles are congruent. This is a fundamental concept in Euclidean geometry used frequently in proving other geometric properties and theorems.
Tips
- Confusing the order of sides and angles. Make sure to identify the correct included angle when using the SAS postulate.
- Not confirming that the side lengths are indeed equal. Always verify the measurements before concluding congruence.
AI-generated content may contain errors. Please verify critical information