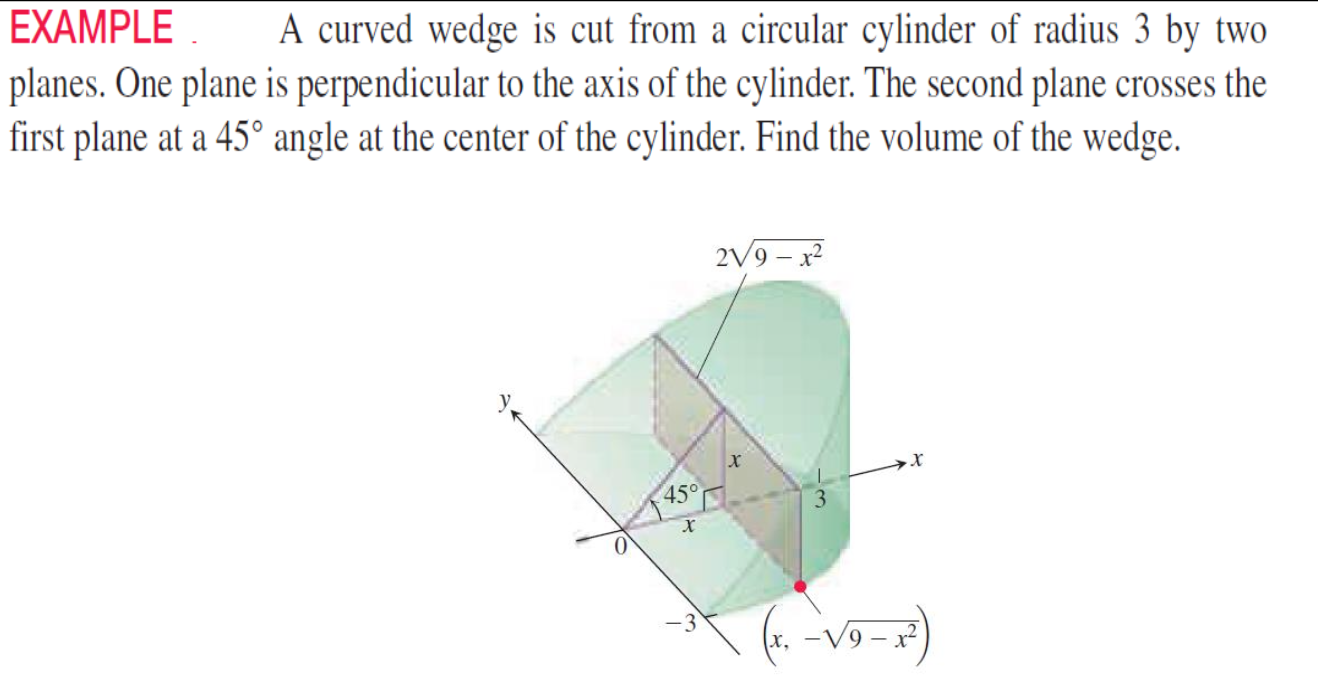
A curved wedge is cut from a circular cylinder of radius 3 by two planes. One plane is perpendicular to the axis of the cylinder. The second plane crosses the first plane at a 45°... A curved wedge is cut from a circular cylinder of radius 3 by two planes. One plane is perpendicular to the axis of the cylinder. The second plane crosses the first plane at a 45° angle at the center of the cylinder. Find the volume of the wedge.
Understand the Problem
The question asks for the volume of a curved wedge cut from a circular cylinder, detailing the conditions of the cuts and the geometry involved. To solve this, we will likely use principles from calculus, particularly integration, given the shape and planes involved.
Answer
The volume of the wedge is $$ V = \frac{27\pi}{8} $$
Answer for screen readers
The volume of the wedge cut from the cylinder is
$$ V = \frac{27\pi}{8} $$
Steps to Solve
-
Understand the geometry of the wedge
The wedge is cut from a circular cylinder with radius 3, where the first plane is perpendicular to the axis. The second plane intersects at a 45° angle. The height of the cylinder is denoted by the limits of integration.
-
Determine the equation of the cylinder
The equation of the circular cylinder can be represented in terms of the radius ( r ):
$$ x^2 + y^2 = 9 $$
This indicates that the maximum allowable ( y ) value (vertical height) at any ( x ) is:
$$ y = \sqrt{9 - x^2} $$
-
Set up the volume integral
The volume ( V ) of the wedge can be determined by integrating the area of the cross-section as we move along the cylinder’s height. The width of the wedge at a height ( y ) from the base (this must be done with respect to ( y )) can be determined by the intersection of the planes.
-
Calculate the limits of integration
The intersection lines can be determined using trigonometric relationships. Given that the plane is at a 45-degree angle:
Since one plane is perpendicular and the second has a slope of -1 (due to the 45° angle):
$$ y = -x + k $$
At the height ( y = 2 ), equate to find the limit ( k ):
$$ 2 = -x + k \implies k = 2 + x $$
-
Perform the volume integral
To find the volume, integrate the area of the wedge:
The area ( A ) of each cross-section at height ( y ) is bounded by the two curves. Then,
$$ A(y) = \int_{-h}^{h} \sqrt{9 - x^2} , dx $$
Here ( h ) is the intersection from step 4 in the bounds of the cylinder.
The volume ( V ) becomes:
$$ V = \int_{0}^{2} A(y) , dy $$
Substitute the previously calculated area and evaluate the integral.
The volume of the wedge cut from the cylinder is
$$ V = \frac{27\pi}{8} $$
More Information
The result provides the volume of a unique wedge shaped by two intersecting planes in a circular cylinder, showcasing the application of both geometric and calculus principles—specifically integration to calculate volume.
Tips
- Not finding the correct limits of integration based on the intersection of the planes.
- Miscalculating the area of the cross-sections, especially under transformations when the angle is involved.
- Forgetting the cylinder's equation when setting up the integration.
AI-generated content may contain errors. Please verify critical information