A circle passes through the origin whose center lies on x^2 + y^2 - Hx - 6y + 10 = 0 and it cuts orthogonally.
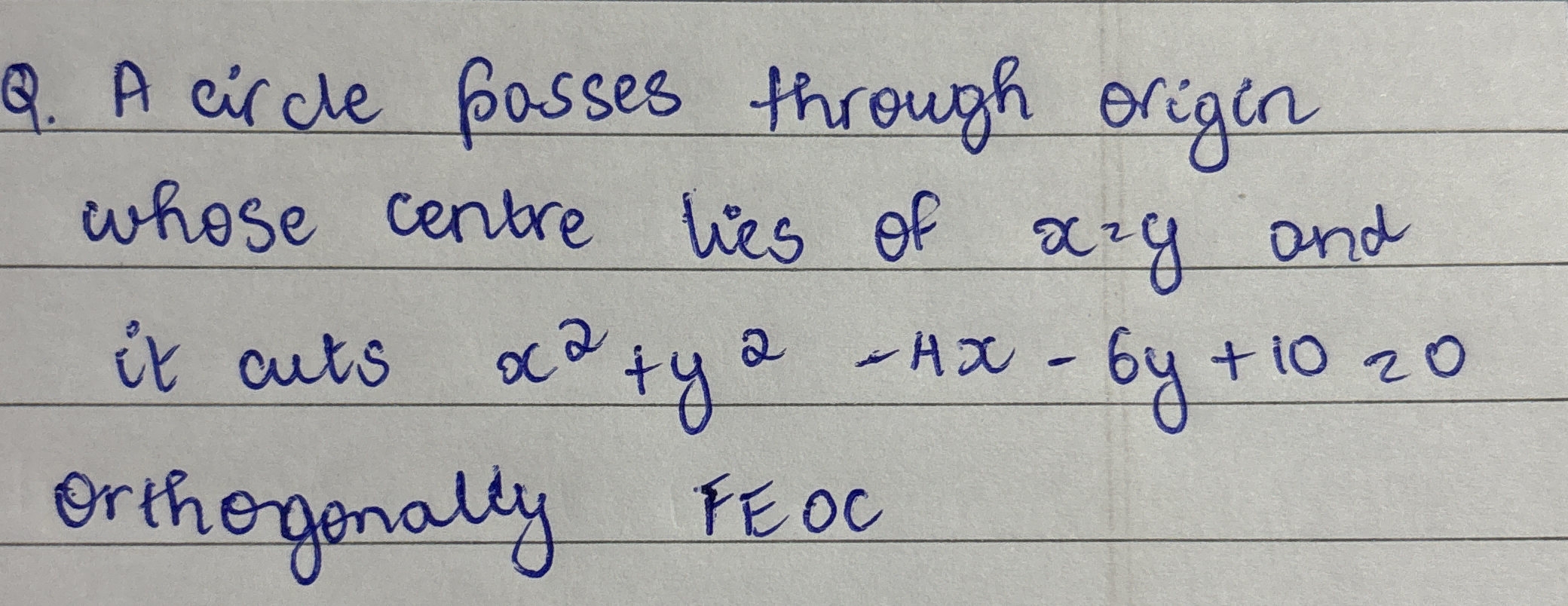
Understand the Problem
The question is asking to find the equation of a circle that passes through the origin and has a center that lies on the line defined by the equation x^2 + y^2 - Hx - 6y + 10 = 0. The phrase 'cuts orthogonally' suggests that the circle intersects another curve or line at right angles, indicating a geometric relationship that needs to be established.
Answer
The equation of the circle is given by: $$ (x - h)^2 + (y - k)^2 = Hh + 6k - 10 $$
Answer for screen readers
The equation of the circle is given by the form: $$ (x - h)^2 + (y - k)^2 = Hh + 6k - 10 $$
Steps to Solve
-
Identify the center of the circle Let the center of the circle be denoted as $(h, k)$. Since the center lies on the curve defined by $x^2 + y^2 - Hx - 6y + 10 = 0$, we substitute $h$ and $k$ into that equation: $$ h^2 + k^2 - Hh - 6k + 10 = 0 $$
-
Use the circle's equation The equation of a circle passing through the origin and having a center at $(h, k)$ is given by: $$ (x - h)^2 + (y - k)^2 = r^2 $$ Since it passes through the origin $(0, 0)$, substituting these values gives: $$ h^2 + k^2 = r^2 $$
-
Orthogonality condition For the circle to intersect orthogonally with the given curve, the condition is that: $$ 2h \cdot H + 2k \cdot 6 = r^2 $$ Substituting $r^2$ from the previous step, we have: $$ 2hH + 12k = h^2 + k^2 $$
-
Formulate equations Now we have the system of equations:
-
$$ h^2 + k^2 - Hh - 6k + 10 = 0 $$
-
$$ 2hH + 12k = h^2 + k^2 $$
-
Solve the system From the first equation, express $h^2 + k^2$ in terms of $h$ and $k$: $$ h^2 + k^2 = Hh + 6k - 10 $$ Substituting into the second equation results in: $$ 2hH + 12k = Hh + 6k - 10 $$
-
Rearranging Rearranging gives: $$ Hh + 6k - 2hH - 12k + 10 = 0 $$ Simplifying leads to: $$ (1 - 2H)h + (6 - 12)k + 10 = 0 $$ Which gives the relation between $h$ and $k$.
-
Final form of circle equation Using the relations deduced, substitute back into the circle equation to express it in standard form.
The equation of the circle is given by the form: $$ (x - h)^2 + (y - k)^2 = Hh + 6k - 10 $$
More Information
This equation denotes a circle with its center at $(h, k)$, which intersects the curve orthogonally and passes through the origin. The parameters $h$ and $k$ are constrained by geometric relations that derive from the original curve equation.
Tips
- Mistaking the coordinates of the center while substituting into the equation of the given curve.
- Forgetting to apply the orthogonality condition, which is crucial for deriving the relationship between parameters.
AI-generated content may contain errors. Please verify critical information