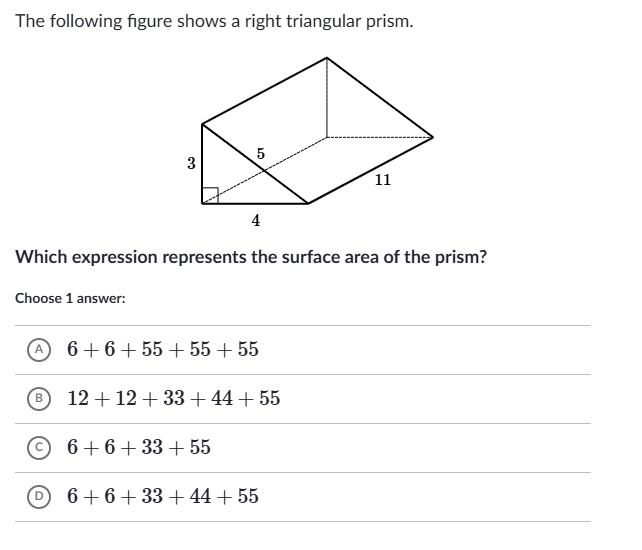
Which expression represents the surface area of the prism?

Steps to Solve

1. Identify the triangular base area The base of the prism is a right triangle. To find the area of this triangle, use the formula: $$ A = \frac{1}{2} \times \text{base} \times \text{height} $$ Here, the base is 4 and the height is 3: $$ A = \frac{1}{2} \times 4 \times 3 = 6 $$

2. Calculate the lateral surface area The lateral surface area consists of three rectangles. Each rectangle's area is calculated as:

• Rectangle 1: Area = Base × Height = 4 × 11 = 44
• Rectangle 2: Area = Height × Height = 3 × 11 = 33
• Rectangle 3: Area = Hypotenuse × Height. The hypotenuse can be calculated using the Pythagorean theorem: $$ \text{Hypotenuse} = \sqrt{4^2 + 3^2} = 5 $$ So, Rectangle 3: Area = 5 × 11 = 55.

3. Sum the areas of all faces Now, add the area of the triangular bases and the lateral areas:

• Area of two triangular bases: $2 \times 6 = 12$
• Lateral areas: $44 + 33 + 55 = 132$

Total surface area is: $$ \text{Total Area} = 12 + 132 = 144 $$

But since the problem asks for the expression representing this surface area, we'll write it in terms of the summed up components: $$ \text{Total Area} = 6 + 6 + 44 + 33 + 55 $$