6x - 7 = 0 and 12x + 4c = 82 are two equations in x. If they have the same solution, then c = ?
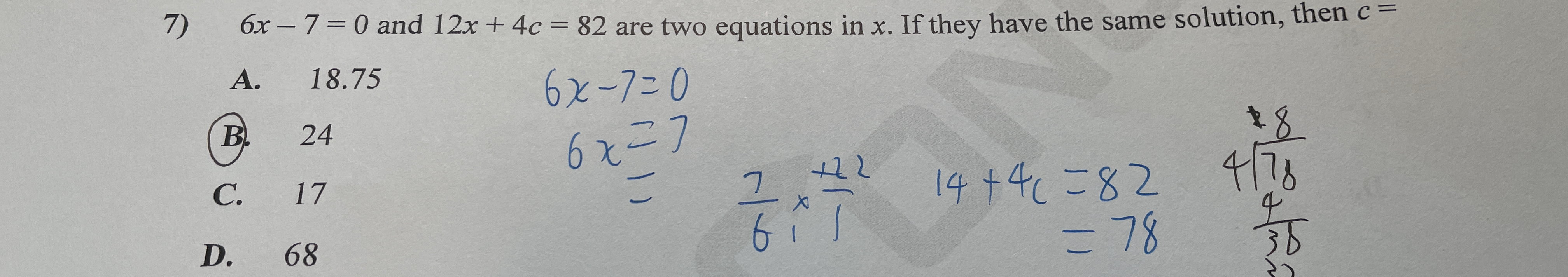
Understand the Problem
The question involves solving a system of equations to find the value of c, given that both equations have the same solution in x. We will solve each equation for x and then equate them to find c.
Answer
$c = 17$
Answer for screen readers
The value of (c) is (17).
Steps to Solve
- Solve the First Equation for x
Start with the equation (6x - 7 = 0).
Add 7 to both sides to isolate the term with (x):
$$6x = 7$$
Next, divide both sides by 6:
$$x = \frac{7}{6}$$
- Set up the Second Equation
Now, look at the second equation (12x + 4c = 82).
We will substitute the value of (x) we found earlier into this equation.
- Substitute x into the Second Equation
Substituting (x = \frac{7}{6}) into the second equation:
$$12\left(\frac{7}{6}\right) + 4c = 82$$
Which simplifies to:
$$14 + 4c = 82$$
- Isolate c
Subtract 14 from both sides:
$$4c = 82 - 14$$
This gives us:
$$4c = 68$$
- Solve for c
Now, divide both sides by 4:
$$c = \frac{68}{4}$$
This simplifies to:
$$c = 17$$
The value of (c) is (17).
More Information
The equation (6x - 7 = 0) gives a solution for (x) that can be substituted into the second equation. Finding a consistent value for (c) ensures both equations share the same (x) solution.
Tips
- Forgetting to isolate (c) properly by not performing the necessary arithmetic operations.
- Miscalculating the simplification of fractions or basic arithmetic.
AI-generated content may contain errors. Please verify critical information