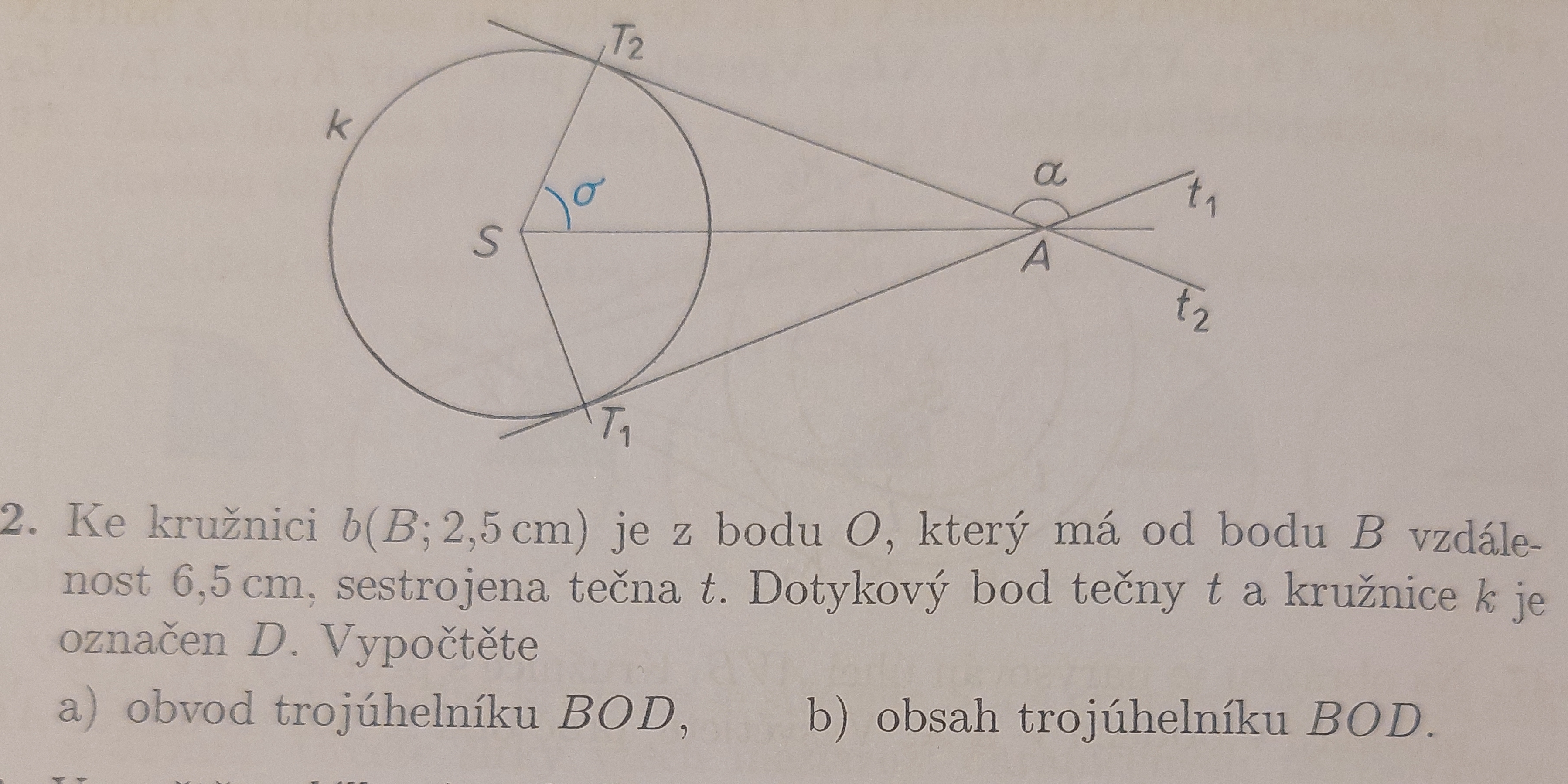
Ke kružnici b(B; 2,5 cm) je z bodu O, který má od bodu B vzdálenost 6,5 cm, sestrojena tečna t. Dotykový bod tečny t a kružnice k je označen D. Vypočtěte a) obvod trojúhelníku BOD,... Ke kružnici b(B; 2,5 cm) je z bodu O, který má od bodu B vzdálenost 6,5 cm, sestrojena tečna t. Dotykový bod tečny t a kružnice k je označen D. Vypočtěte a) obvod trojúhelníku BOD, b) obsah trojúhelníku BOD.
Understand the Problem
The question is asking to calculate two geometric properties: the perimeter of triangle BOD and the area of triangle BOD, using information about tangents and distances related to a circle.
Answer
a) $15 \, \text{cm}$, b) $7,5 \, \text{cm}^2$
Answer for screen readers
a) Obvod trojúhelníku BOD je $15 , \text{cm}$.
b) Obsah trojúhelníku BOD je $7,5 , \text{cm}^2$.
Steps to Solve
- Určení délek stran trojúhelníku BOD
V trojúhelníku BOD máme:
- ( r = 2,5 , \text{cm} ) (poloměr kružnice)
- ( OB = 6,5 , \text{cm} ) (vzdálenost bodu O od bodu B)
- Délka úsečky ( BD ) je rovna poloměru kružnice: ( BD = 2,5 , \text{cm} ).
- Délku úsečky ( OD ) zjistíme pomocí Pythagorovy věty, kde ( OD ) je kolmá výška z O na BD. Vytvoříme pravoúhlý trojúhelník OBD.
- Vypočtení délky úsečky OD
Podle Pythagorovy věty:
$$
OD = \sqrt{OB^2 - BD^2} = \sqrt{(6,5)^2 - (2,5)^2}
$$
Vypočítáme jednotlivé čtverce:
$$
OB^2 = 6,5^2 = 42,25
$$
$$
BD^2 = 2,5^2 = 6,25
$$
Teď dosadíme do výrazu pro délku ( OD ):
$$
OD = \sqrt{42,25 - 6,25} = \sqrt{36} = 6 , \text{cm}
$$
- Vypočtení obvodu trojúhelníku BOD
Obvod trojúhelníku spočítáme jako součet délek všech stran:
$$
s = OB + OD + BD = 6,5 + 6 + 2,5
$$
Vypočteme:
$$
s = 15 , \text{cm}
$$
- Vypočtení obsahu trojúhelníku BOD
Obsah trojúhelníku ( BOD ) spočítáme pomocí vzorce pro obsah pravoúhlého trojúhelníku:
$$
S = \frac{1}{2} \times BD \times OD
$$
Dosadíme:
$$
S = \frac{1}{2} \times 2,5 \times 6
$$
Vypočteme:
$$
S = \frac{1}{2} \times 15 = 7,5 , \text{cm}^2
$$
a) Obvod trojúhelníku BOD je $15 , \text{cm}$.
b) Obsah trojúhelníku BOD je $7,5 , \text{cm}^2$.
More Information
Obvod trojúhelníku je celková délka jeho stran, zatímco obsah určuje plochu, kterou trojúhelník zaujímá. Pythagorova věta je užitečná při výpočtech v pravoúhlých trojúhelnících.
Tips
- Záměna délek stran: Zajistit, že správně přiřazujete délky stran k správným bodům trojúhelníku.
- Chyby ve výpočtech čtverců: Důležité je pečlivě vypočítat čtverce délek.
AI-generated content may contain errors. Please verify critical information