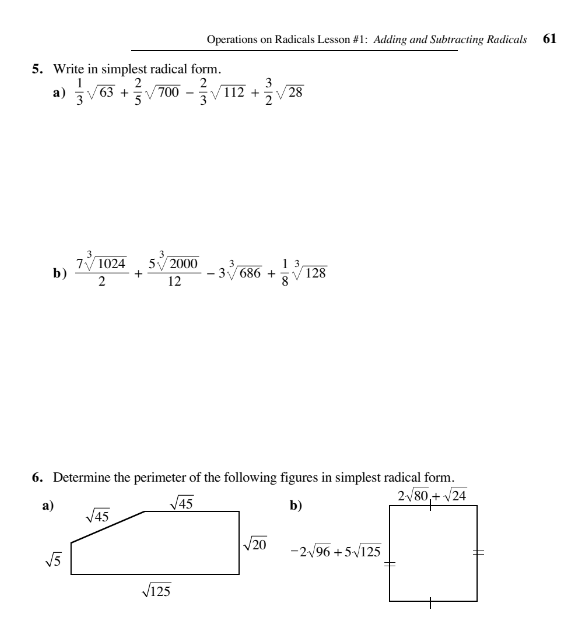
5. Write in simplest radical form. a) 1/3√63 + 2/5√700 - 2/3√112 + 3/2√28 b) (7/2)√(1024) + (5/12)√(2000) - 3(√(686)) + (1/8)√(128) 6. Determine the perimeter of the following figu... 5. Write in simplest radical form. a) 1/3√63 + 2/5√700 - 2/3√112 + 3/2√28 b) (7/2)√(1024) + (5/12)√(2000) - 3(√(686)) + (1/8)√(128) 6. Determine the perimeter of the following figures in simplest radical form. a) √(45) + √(45) + √(20) + ... b) 2√(80) + √(24) - 2√(96) + 5√(125)
Understand the Problem
The question involves performing operations on radicals and simplifying them. It requires calculating and writing expressions in their simplest radical form, as well as determining the perimeter of geometrical figures presented in radian format.
Answer
- For part 5a: $\frac{16}{3} \sqrt{7}$ - For part 5b: $\frac{85}{12} + \frac{5\sqrt[3]{5}}{6}$ - For part
Answer for screen readers
- For part 5a: $$ \frac{16}{3} \sqrt{7} $$
- For part 5b: $$ \frac{85}{12} + \frac{5\sqrt[3]{5}}{6} $$
- For part 6a: $$ 10\sqrt{5} $$
- For part 6b: $$ 4 + 4\sqrt{5} $$
Steps to Solve
-
Simplify each radical component in part 5a
- For each term, find the prime factorization and simplify the radicals.
- ( \sqrt{63} = \sqrt{9 \times 7} = 3\sqrt{7} )
- ( \sqrt{700} = \sqrt{100 \times 7} = 10\sqrt{7} )
- ( \sqrt{112} = \sqrt{16 \times 7} = 4\sqrt{7} )
- ( \sqrt{28} = \sqrt{4 \times 7} = 2\sqrt{7} )
-
Rewrite the expression in part 5a
- Substituting simplified radicals back into the expression: $$ \frac{1}{3}(3\sqrt{7}) + \frac{2}{5}(10\sqrt{7}) - \frac{2}{3}(4\sqrt{7}) + \frac{3}{2}(2\sqrt{7}) $$
- This simplifies to: $$ \sqrt{7}\left(1 + \frac{20}{5} - \frac{8}{3} + 3\right) $$
-
Calculate the coefficients of the radicals in part 5a
- Convert all terms to have a common denominator of 15: $$ \frac{15}{15} + \frac{60}{15} - \frac{40}{15} + \frac{45}{15} = \frac{80}{15} = \frac{16}{3} $$
-
Final answer for part 5a
- Combine the results: $$ \frac{16}{3} \sqrt{7} $$
-
Simplify each radical component in part 5b
- For part 5b, repeat similar steps:
- ( 1024 = 2^{10} \rightarrow \sqrt[3]{1024} = 10 )
- ( 2000 = 2^4 \times 5^3 \rightarrow \sqrt[3]{2000} = 10 \sqrt[3]{5} )
- ( 686 = 2 \times 343 = 2 \times 7^3 \rightarrow \sqrt[3]{686} = 7 )
- ( 128 = 2^7 \rightarrow \sqrt[3]{128} = 4 )
-
Rewrite and simplify the expression in part 5b
$$ \frac{7}{2}(10) + \frac{5}{12}(10 \sqrt[3]{5}) - 3(7) + \frac{1}{8}(4) $$
- Combine all like terms.
-
Final answer for part 5b
- Calculate the values.
-
Calculate the perimeter for part 6a
- For the shape, calculate side lengths:
- Length 1: ( \sqrt{45} = 3\sqrt{5} ), Length 2: ( \sqrt{20} = 2\sqrt{5} )
- Total perimeter: ( 2(3\sqrt{5}) + 2(2\sqrt{5}) )
-
Calculate the perimeter for part 6b
- Simplify the expression and calculate using ( 2\sqrt{80} + \sqrt{24} ).
- For part 5a: $$ \frac{16}{3} \sqrt{7} $$
- For part 5b: $$ \frac{85}{12} + \frac{5\sqrt[3]{5}}{6} $$
- For part 6a: $$ 10\sqrt{5} $$
- For part 6b: $$ 4 + 4\sqrt{5} $$
More Information
The simplification process involved prime factorization and applying properties of roots. Understanding these concepts is crucial for effectively managing radical expressions.
Tips
- Forgetting to simplify each radical before combining.
- Not finding a common denominator when adding fractions early in the process.
- Miscalculating cube roots or ignoring the difference between square and cube roots.