5 - 2(3 - x) = 4x + 10
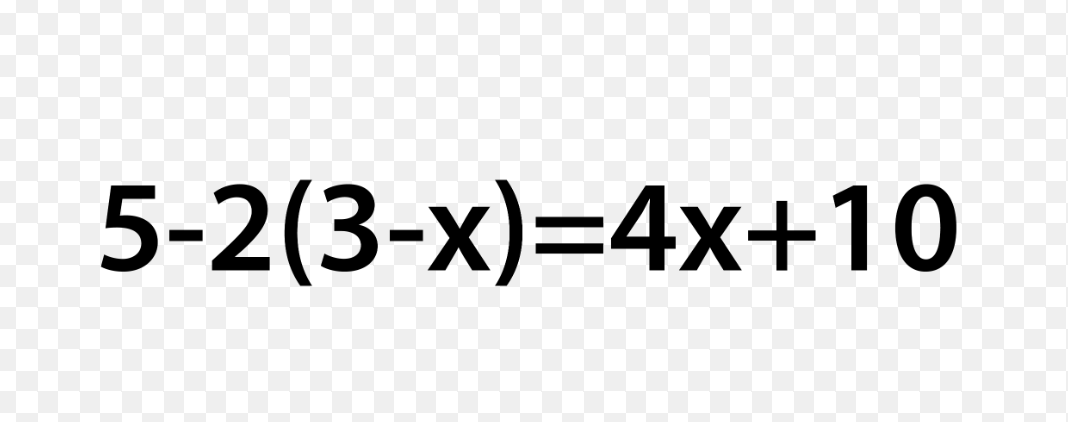
Understand the Problem
The question is asking to solve the equation 5 - 2(3 - x) = 4x + 10. This involves simplifying both sides and isolating the variable x.
Answer
$x = -\frac{11}{2}$
Answer for screen readers
The solution is $x = -\frac{11}{2}$.
Steps to Solve
-
Expand the equation To simplify the equation, distribute the $-2$ across the $(3 - x)$ on the left side: $$ 5 - 2(3 - x) = 4x + 10 $$ This becomes: $$ 5 - 6 + 2x = 4x + 10 $$
-
Combine like terms Combine the constants on the left side: $$ -1 + 2x = 4x + 10 $$
-
Isolate the variable To isolate $x$, subtract $2x$ from both sides: $$ -1 = 2x + 10 $$
-
Further isolate $x$ Now, subtract $10$ from both sides: $$ -11 = 2x $$
-
Solve for $x$ Finally, divide both sides by $2$: $$ x = -\frac{11}{2} $$
The solution is $x = -\frac{11}{2}$.
More Information
The solution to the equation shows how to handle equations involving parentheses and isolate a variable effectively. The answer $-\frac{11}{2}$ can also be expressed as -5.5 in decimal form.
Tips
- Not distributing correctly: Often, students forget to apply the negative sign while distributing, leading to incorrect simplifications. To avoid this, double-check each step while distributing.
- Combining terms inaccurately: Ensure you only combine like terms; check that you’re not mistakenly adding or subtracting different types.
AI-generated content may contain errors. Please verify critical information