4log_x + 5log_x - log_x z - log_b.
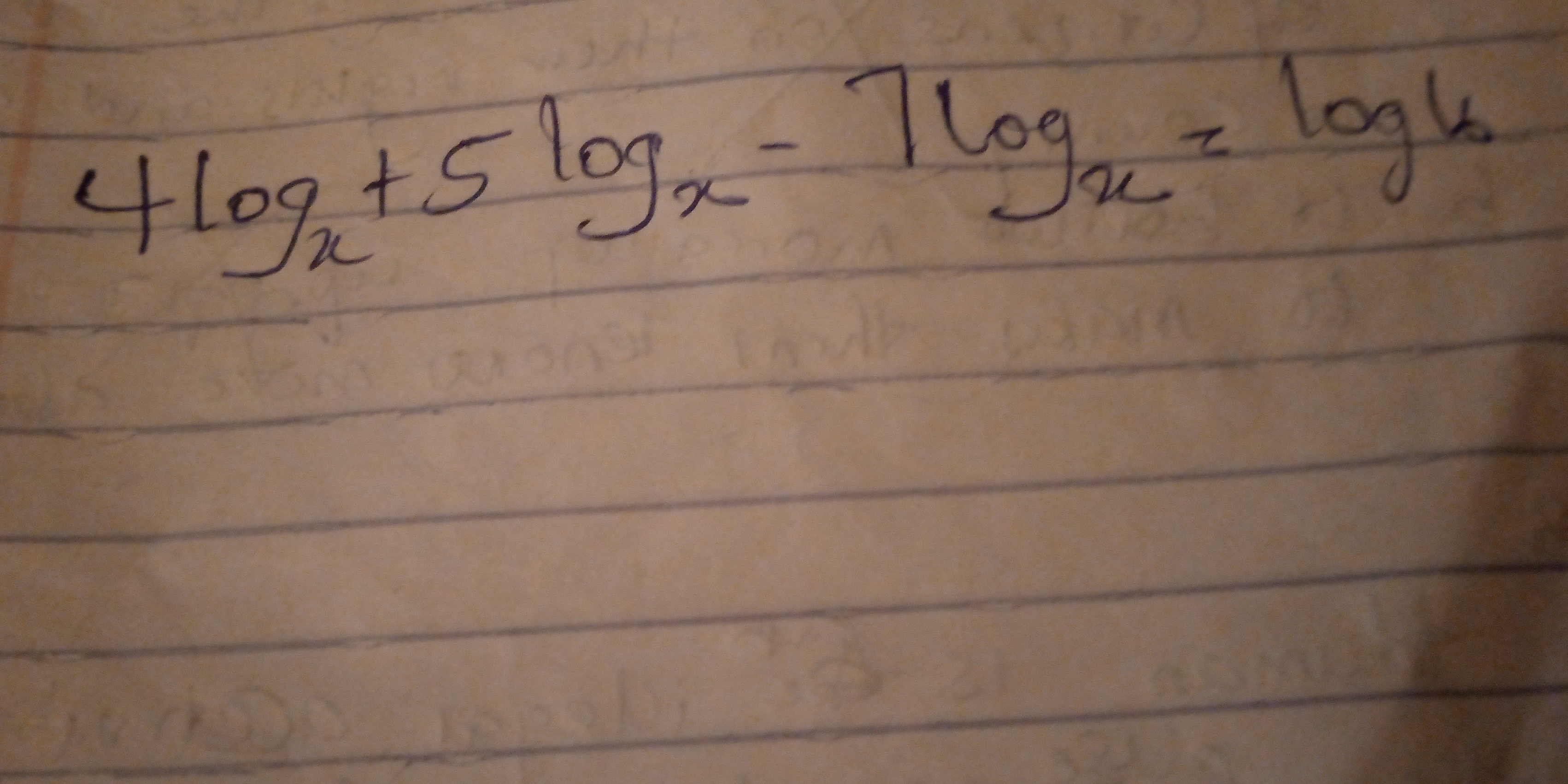
Understand the Problem
The question is asking to simplify or solve the expression involving logarithms: 4log_x + 5log_x - log_x z - log_b.
Answer
The simplified expression is $$ \log_x\left(\frac{x^9}{z}\right) - \log_b $$
Answer for screen readers
The simplified expression is
$$ \log_x\left(\frac{x^9}{z}\right) - \log_b $$
Steps to Solve
- Combine Like Terms We begin by combining the logarithmic terms. Since $4 \log_x + 5 \log_x = 9 \log_x$, we can simplify the expression:
$$ 9 \log_x - \log_x z - \log_b $$
- Use the Logarithm Property We can apply the properties of logarithms. The property states that $a \log_b(c) = \log_b(c^a)$ and the subtraction property states that $\log_b(a) - \log_b(c) = \log_b\left(\frac{a}{c}\right)$. Thus, we can rewrite the expression:
$$ 9 \log_x - \log_x z = 9 \log_x - \log_x(z) = \log_x\left(x^9\right) - \log_x(z) $$
- Apply the Subtraction Property Now apply the subtraction property of logarithms:
$$ \log_x\left(\frac{x^9}{z}\right) $$
- Combine with the Remaining Logarithm Next, we need to include the $-\log_b$ term. Given that we cannot combine terms with different bases directly, we will denote it as it is:
$$ \log_x\left(\frac{x^9}{z}\right) - \log_b $$
The simplified expression is
$$ \log_x\left(\frac{x^9}{z}\right) - \log_b $$
More Information
This result can be useful in various contexts, especially in calculus and when dealing with logarithmic equations and inequalities. Understanding the properties of logarithms is crucial for simplifying logarithmic expressions effectively.
Tips
- Forgetting Properties of Logarithms: Make sure to apply the logarithm properties correctly, such as combining and simplifying logarithmic expressions.
- Trying to Combine Different Bases: Logarithms with different bases cannot be combined directly. Be cautious with terms that involve different bases.
AI-generated content may contain errors. Please verify critical information