Jika √(5p + √(5p + √(5p + ...)) = 6, maka nilai p adalah ...
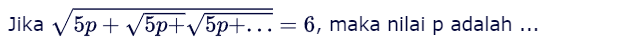
Understand the Problem
Pertanyaan ini meminta kita untuk mencari nilai p dari persamaan berulang yang melibatkan akar kuadrat. Kita perlu menyelesaikan persamaan tersebut untuk menemukan nilai p.
Answer
$p = 6$
Answer for screen readers
$p = 6$
Steps to Solve
-
Menyatakan Persamaan Kita mulai dengan menyatakan persamaan yang diberikan. Misalkan $x$ adalah nilai persamaan tersebut, kita punya: $$ x = \sqrt{5p + x} $$
-
Mengganti dengan Nilai yang Diberikan Kita tahu dari soal bahwa $x = 6$. Dengan begitu, kita substitusi nilai ini ke dalam persamaan: $$ 6 = \sqrt{5p + 6} $$
-
Mengkuadratkan Kedua Sisi Untuk menghilangkan akar kuadrat, kita kuadratkan kedua sisi dari persamaan: $$ 6^2 = 5p + 6 $$ $$ 36 = 5p + 6 $$
-
Menyelesaikan untuk p Selanjutnya, kita akan menyelesaikan untuk $p$. Pertama, kita kurangi $6$ dari kedua sisi: $$ 36 - 6 = 5p $$ $$ 30 = 5p $$
-
Membagi Kedua Sisi Kemudian, kita bagi kedua sisi dengan $5$ untuk menemukan nilai $p$: $$ p = \frac{30}{5} $$ $$ p = 6 $$
$p = 6$
More Information
Nilai yang ditemukan, yaitu $p = 6$, menunjukkan bahwa ketika kita substitusi kembali ke dalam persamaan awal, semua kasukuran akan sesuai, membuktikan bahwa $p$ sudah benar.
Tips
- Mengabaikan Sisi Negatif: Ketika mengkuadratkan, mungkin ada yang melupakan bahwa $ \sqrt{x} $ tidak negatif. Namun, dalam konteks ini kita hanya mempertimbangkan solusi positif karena nilai $x$.
- Kesalahan dalam Distribusi: Pastikan saat menyederhanakan, distribusi atau langkah-langkah matematika tetap hati-hati agar tidak salah.
AI-generated content may contain errors. Please verify critical information