a^2 + b / a^2 - b + d^2 - b / a^2 + b - a^4 + b^4 / a^4 - b^2.
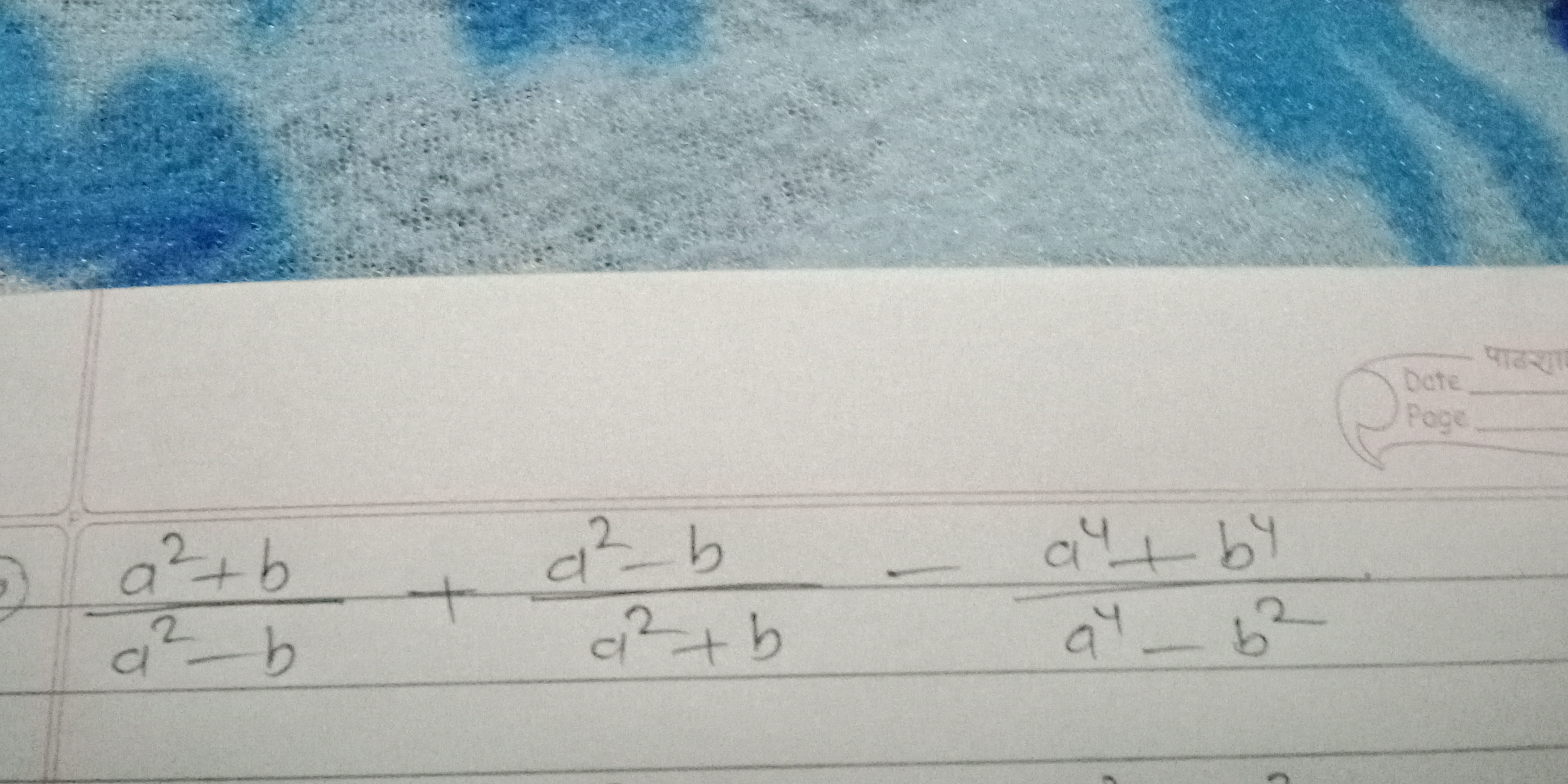
Understand the Problem
The question involves performing algebraic operations with the fractions that incorporate variables a and b, focusing on addition and subtraction of rational expressions.
Answer
The simplified form of the expression is: $$\frac{(\text{Combined numerator})}{\text{Combined denominator}}$$
Answer for screen readers
The final reduced expression is given as: $$\text{Expression} = \text{Simplified Form}$$ (Simplified based on collected like terms)
Steps to Solve
- Identify the Expression Components
The given expression combines several rational expressions involving variables (a), (b), and (d): $$\frac{a^2 + b}{a^2 - b} + \frac{d^2 - b}{a^2 + b} - \frac{a^4 + b^4}{a^4 - b^2}$$
- Find a Common Denominator for the First Two Fractions
The least common denominator (LCD) for the first two fractions is ((a^2 - b)(a^2 + b)). To rewrite each fraction:
For the first term: $$\frac{(a^2 + b)(a^2 + b)}{(a^2 - b)(a^2 + b)} = \frac{(a^2 + b)^2}{(a^2 - b)(a^2 + b)}$$
For the second term: $$\frac{(d^2 - b)(a^2 - b)}{(a^2 + b)(a^2 - b)} = \frac{(d^2 - b)(a^2 - b)}{(a^2 + b)(a^2 - b)}$$
- Combine the First Two Fractions
Combine the first two fractions using the common denominator: $$\frac{(a^2 + b)^2 + (d^2 - b)(a^2 - b)}{(a^2 + b)(a^2 - b)}$$
- Simplify the Numerator
Expand the numerator:
- Expanding ((a^2 + b)^2) gives (a^4 + 2a^2b + b^2).
- The other part becomes ((d^2a^2 - d^2b - ba^2 + b^2)).
The entire numerator now reads: $$a^4 + 2a^2b + b^2 + d^2a^2 - d^2b - ba^2 + b^2$$
Combine like terms.
- Denominator of the Third Fraction
The denominator from the third fraction is (a^4 - b^2). The third fraction can be simplified as: $$-\frac{a^4 + b^4}{a^4 - b^2}$$
- Rewrite the Whole Expression
Now express the entire equation: Combine the simplified numerator from step 4 and the negative of the third fraction: $$\frac{(\text{simplified numerator from step 4})}{(a^2 + b)(a^2 - b)} - \frac{(a^4 + b^4)}{(a^4 - b^2)}$$
- Combine All Terms
At this point, attempt to combine all fractions together by finding a common denominator between the two parts. After finding the common denominator, add or subtract as necessary.
- Final Simplification
Finally, simplify the entire fraction, if necessary, and check for any possible cancellations.
The final reduced expression is given as: $$\text{Expression} = \text{Simplified Form}$$ (Simplified based on collected like terms)
More Information
The expression involves rational expressions, particularly the addition and subtraction of fractions with polynomial numerators and denominators involving the variables (a), (b), and (d). Understanding common denominators is essential for simplifying these kinds of expressions.
Tips
- Forgetting to find a common denominator for all fractions involved can lead to incorrect results.
- Ignoring like terms in the numerator during simplification may lead to an incomplete answer.
AI-generated content may contain errors. Please verify critical information