4. (x + 2)(x - 2) / (x - 1)(x + 1) = 4 / 5
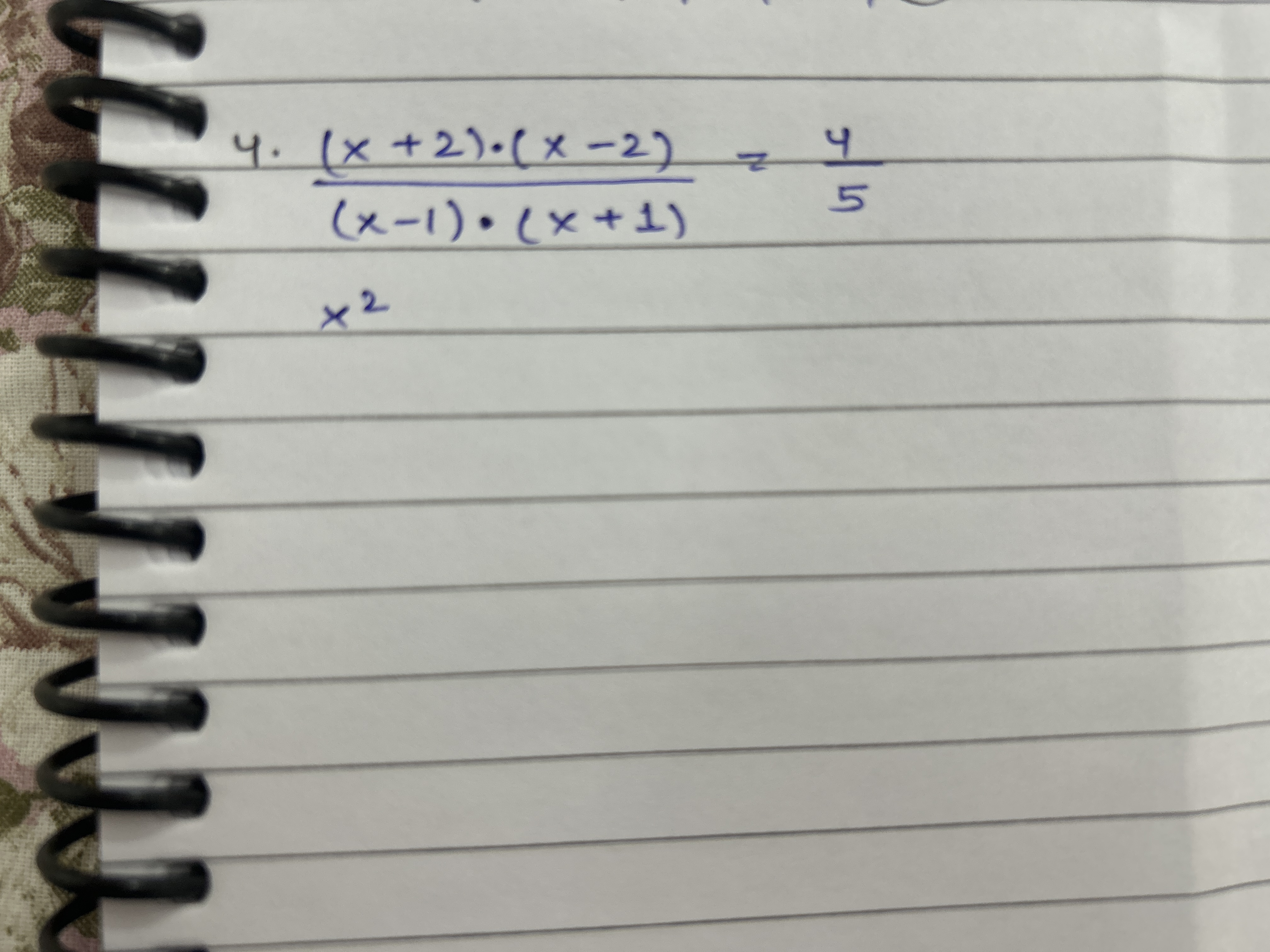
Understand the Problem
The question is asking to solve an equation that involves variables and polynomial expressions. It appears to involve a rational equation where the left-hand side equals the right-hand side. We will need to identify the variables and simplify or solve the equation step by step.
Answer
No real solutions.
Answer for screen readers
There are no real solutions for the equation.
Steps to Solve
-
Identify the given equation The equation is given as: $$ \frac{(x+2)(x-2)}{x^2} = \frac{(x-1)(x+1)}{5} $$
-
Cross-multiply to eliminate fractions To eliminate the fractions, we can cross-multiply: $$ 5(x+2)(x-2) = (x-1)(x+1)x^2 $$
-
Expand both sides Now we need to expand both sides of the equation: Left side: $$ 5((x+2)(x-2)) = 5(x^2 - 4) = 5x^2 - 20 $$
Right side: $$ (x-1)(x+1) = x^2 - 1 $$ Thus, $$ (x^2 - 1)x^2 = x^4 - x^2 $$
- Set the equation to zero Combine the terms: $$ 5x^2 - 20 = x^4 - x^2 $$
Rearranging gives: $$ 0 = x^4 - 6x^2 + 20 $$
-
Form a standard polynomial Rearranging the equation gives: $$ x^4 - 6x^2 + 20 = 0 $$
-
Use substitution for quadratic form Let $y = x^2$. The equation becomes: $$ y^2 - 6y + 20 = 0 $$
-
Apply the quadratic formula Using the quadratic formula (y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}): For the current equation, where (a = 1), (b = -6), and (c = 20): $$ y = \frac{6 \pm \sqrt{(-6)^2 - 4(1)(20)}}{2(1)} $$
-
Calculate the discriminant Calculate the discriminant: $$ (-6)^2 - 4(1)(20) = 36 - 80 = -44 $$
Since the discriminant is negative, there are no real solutions for (y), and consequently no real solutions for (x).
There are no real solutions for the equation.
More Information
The equation involves rational expressions that, when simplified and combined, result in a polynomial with a negative discriminant. This indicates no real roots exist, so all solutions are complex.
Tips
- Not correctly simplifying fractions before cross-multiplying.
- Neglecting to correctly apply the quadratic formula, particularly when determining the discriminant.
AI-generated content may contain errors. Please verify critical information