(3x + 5)(x^2 - 10x + 2) - (2x - 1)(x^2 - 3x - 7)
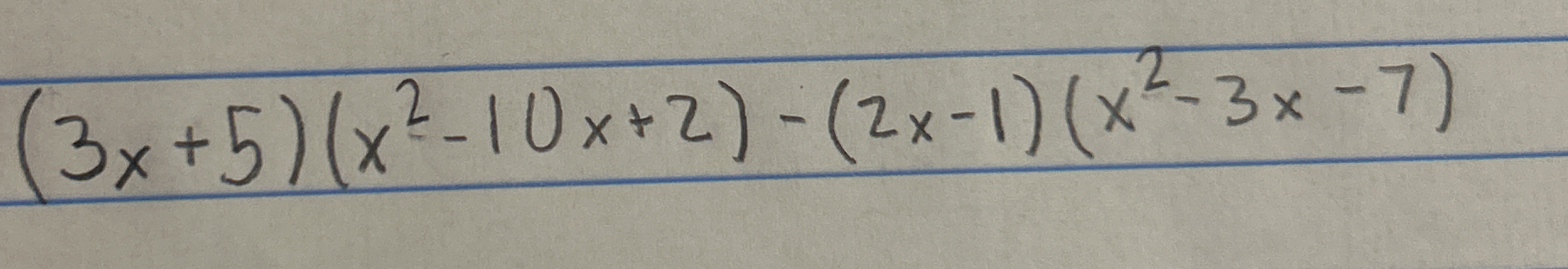
Understand the Problem
The question involves performing algebraic operations, specifically multiplying and subtracting polynomial expressions. The problem appears to require simplifying or finding a specific value from these expressions.
Answer
The simplified expression is $x^3 - 18x^2 - 33x + 3$.
Answer for screen readers
The final answer is:
$$ x^3 - 18x^2 - 33x + 3 $$
Steps to Solve
- Expand the First Expression
We begin by expanding the first part: $(3x + 5)(x^2 - 10x + 2)$.
Using the distributive property: [ 3x \cdot (x^2 - 10x + 2) + 5 \cdot (x^2 - 10x + 2) ] This simplifies to: [ 3x^3 - 30x^2 + 6x + 5x^2 - 50x + 10 = 3x^3 - 25x^2 - 44x + 10 ]
- Expand the Second Expression
Next, we expand the second part: $(2x - 1)(x^2 - 3x - 7)$. [ 2x \cdot (x^2 - 3x - 7) - 1 \cdot (x^2 - 3x - 7) ] This simplifies to: [ 2x^3 - 6x^2 - 14x - x^2 + 3x + 7 = 2x^3 - 7x^2 - 11x + 7 ]
- Combine the Polynomials
We now combine the results from step 1 and step 2, along with the subtraction: [ (3x^3 - 25x^2 - 44x + 10) - (2x^3 - 7x^2 - 11x + 7) ] Distributing the negative sign: [ 3x^3 - 25x^2 - 44x + 10 - 2x^3 + 7x^2 + 11x - 7 ]
- Combine Like Terms
Next, we combine like terms: [ (3x^3 - 2x^3) + (-25x^2 + 7x^2) + (-44x + 11x) + (10 - 7) ] This results in: [ x^3 - 18x^2 - 33x + 3 ]
The final answer is:
$$ x^3 - 18x^2 - 33x + 3 $$
More Information
The resulting polynomial represents the algebraic expression simplified after performing the necessary expansions and combining like terms. Each term provides information about the degrees of the polynomial, with $x^3$ being the highest degree.
Tips
- Forgetting to distribute the negative sign when subtracting the second polynomial.
- Neglecting to combine like terms properly can lead to errors in the final expression.
AI-generated content may contain errors. Please verify critical information