20 ml of 4(N) H2SO4 is mixed with 80 ml of 0.5(N) NaOH solution. What is the nature and strength of the final solution?
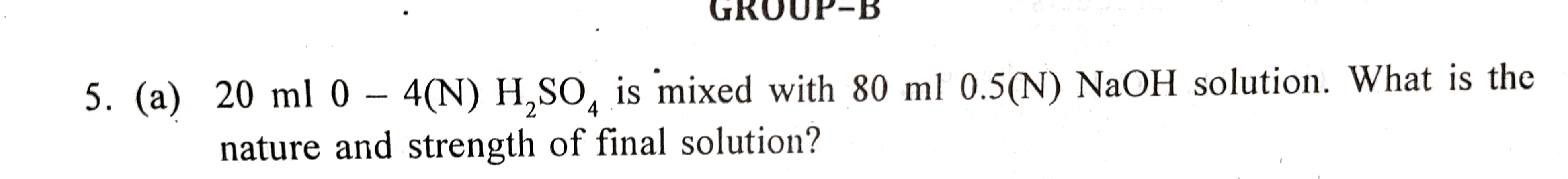
Understand the Problem
The question is asking for the nature and strength of the final solution when a specified volume of sulfuric acid is mixed with a specified volume of sodium hydroxide solution. This involves understanding acid-base reactions and calculating the resultant concentration.
Answer
The solution is acidic with a concentration of $0.6 \, \
Answer for screen readers
The final solution is acidic with a concentration of $0.6 , \text{N}$ H(_2)SO(_4).
Steps to Solve
- Calculate the equivalents of H(_2)SO(_4
First, we find the number of equivalents of sulfuric acid. The normality (N) of H(_2)SO(_4) is given as 4 N, and the volume is 20 ml.
The formula to calculate equivalents is: $$ \text{Equivalents} = \text{Normality} \times \text{Volume (L)} $$
Converting 20 ml to liters: $$ 20 \text{ ml} = 0.020 \text{ L} $$
Now calculate the equivalents: $$ \text{Equivalents of H}_2\text{SO}_4 = 4 , \text{N} \times 0.020 , \text{L} = 0.08 , \text{equivalents} $$
- Calculate the equivalents of NaOH
Next, we find the number of equivalents of sodium hydroxide. The normality of NaOH is 0.5 N, and the volume is 80 ml.
Convert 80 ml to liters: $$ 80 \text{ ml} = 0.080 \text{ L} $$
Now calculate the equivalents: $$ \text{Equivalents of NaOH} = 0.5 , \text{N} \times 0.080 , \text{L} = 0.04 , \text{equivalents} $$
- Determine the limiting reactant
Now, we compare the equivalents of both solutions. The reaction for H(_2)SO(_4) and NaOH is: $$ H_2SO_4 + 2 NaOH \rightarrow Na_2SO_4 + 2 H_2O $$
From the reaction, 1 equivalent of H(_2)SO(_4) reacts with 2 equivalents of NaOH.
Since we have 0.08 equivalents of H(_2)SO(_4), it can react with: $$ 0.08 \times 2 = 0.16 , \text{equivalents of NaOH} $$
However, we only have 0.04 equivalents of NaOH, which means NaOH is the limiting reactant.
- Calculate the excess acid
Now determine how much H(_2)SO(_4) remains after the reaction. Since 0.04 equivalents of NaOH will react with half of their equivalents of H(_2)SO(_4): $$ \text{Required equivalents of H}_2SO_4 = 0.04 \times \frac{1}{2} = 0.02 , \text{equivalents} $$
Thus, the remaining equivalents of H(_2)SO(_4): $$ \text{Excess H}_2SO_4 = 0.08 - 0.02 = 0.06 , \text{equivalents} $$
- Determine the final nature of the solution
Since there is excess H(_2)SO(_4) left after the reaction, the solution will be acidic.
To find the final concentration of H(_2)SO(_4) in the total volume of the solution: Total volume = 20 ml + 80 ml = 100 ml = 0.1 L
Final concentration of H(_2)SO(_4): $$ \text{Final concentration} = \frac{0.06}{0.1} = 0.6 , \text{N} $$
The final solution is acidic with a concentration of $0.6 , \text{N}$ H(_2)SO(_4).
More Information
In this problem, we analyzed the neutralization reaction between sulfuric acid and sodium hydroxide to determine the resulting nature and strength of the solution. The strong acid (H(_2)SO(_4)) remained in excess after reacting with the weak base (NaOH), indicating that the solution is acidic.
Tips
- Miscalculating the volume in liters; ensure conversions from ml to L are correct.
- Failing to recognize the stoichiometric coefficients in balancing the acid-base reaction.
- Confusing normality with molarity; remember that normality accounts for the number of reactive units.
AI-generated content may contain errors. Please verify critical information