(2^{-1})^{-3}
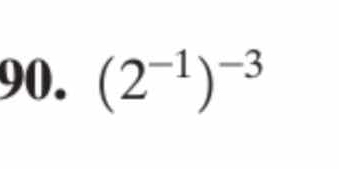
Understand the Problem
The question is asking to simplify the expression (2^{-1})^{-3}. This will involve applying the rules of exponents.
Answer
The value of $(2^{-1})^{-3}$ is $8$.
Answer for screen readers
The simplified expression is $8$.
Steps to Solve
-
Apply the Rule of Exponents for Powers We have the expression $(2^{-1})^{-3}$. When raising a power to another power, we multiply the exponents. Therefore, we can rewrite the expression as: $$(2^{-1})^{-3} = 2^{-1 \cdot -3} = 2^{3}$$
-
Simplify the Exponents Now we simplify $2^{3}$. This means we calculate: $$2^{3} = 2 \times 2 \times 2 = 8$$
The simplified expression is $8$.
More Information
When simplifying exponents, remember to multiply the exponents when raising a power to another power. In this case, a negative exponent indicates the reciprocal, but since we took it to a negative exponent again, it became positive.
Tips
- Mistaking Negative Exponents: A common mistake is to forget that taking a power to a negative exponent involves changing the sign of the exponent. Always remember that $a^{-n} = \frac{1}{a^n}$.
- Multiplying Instead of Reducing: Sometimes, students may confuse the operations and add or incorrectly handle the exponents instead of multiplying.
AI-generated content may contain errors. Please verify critical information