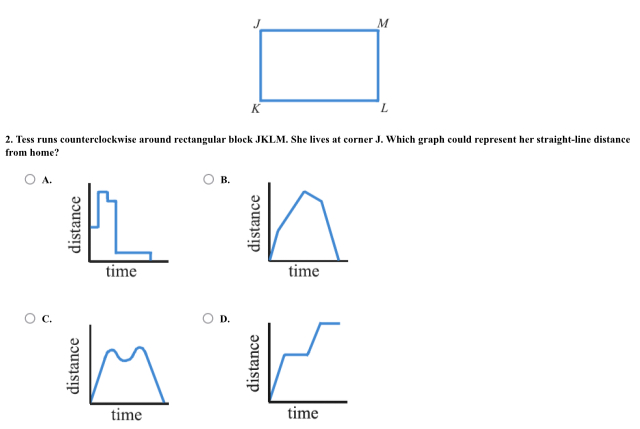
Tess runs counterclockwise around rectangular block JKLM. She lives at corner J. Which graph could represent her straight-line distance from home?

Understand the Problem

The question is asking which graph accurately represents Tess's changing straight-line distance from her home as she runs counterclockwise around a rectangular block. It requires an understanding of distance versus time in relation to her movement around the shape.

Answer

B

Steps to Solve

Understanding the Path Tess starts at corner J and runs counterclockwise around the rectangular block. The distance from her home (corner J) will change as she moves around the block.
Identifying Key Points As Tess runs, her distance from home will:

Decrease as she moves along side JK and KL.
Reach a minimum when she is at corner K.
Increase again as she moves from K to L.
Continue to increase as she moves from L to M.
Finally, decrease again as she moves from M back to J.

Analyzing Each Graph

Graph A: This graph shows a sudden drop followed by a flat distance, which doesn’t match Tess's movement.
Graph B: This graph increases and then decreases, which could represent her distance, especially as she approaches the corners.
Graph C: This graph has a flat distance for a period, suggesting she stops, which is not correct.
Graph D: This graph shows a steady increase, which does not represent her running around the block.

Conclusion The graph that best represents Tess's changing distance from home is the one that properly depicts the segments where her distance increases and decreases.

The correct answer is B, which represents Tess's changing straight-line distance from home as she runs counterclockwise.

More Information

Graph B represents the dynamic nature of Tess’s movement around the block, reflecting the increase and decrease in her distance from home. As she moves toward each corner and around the block, her distance varies continuously.

Tips

Misinterpreting the flat segments in some graphs as stops, while Tess is continuously running.
Not recognizing how distance decreases as she approaches the nearest points to her home.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!