∫(1/(x√(x² - a²))) dx = (1/a) sec⁻¹(x/a) + c
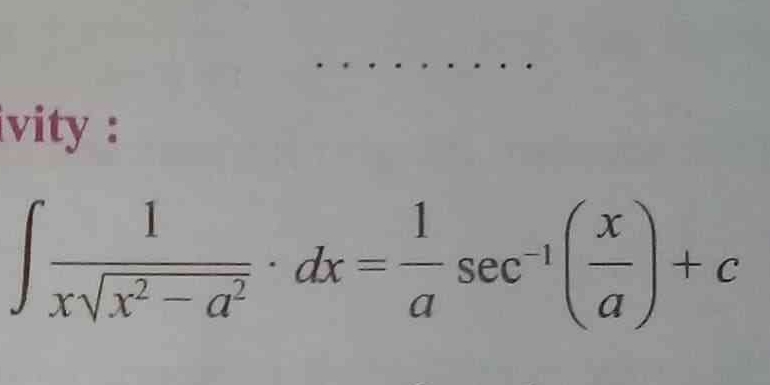
Understand the Problem
The question provides an integral expression and claims that it equals a specific formula involving the secant inverse function. The high-level approach will involve verifying the integral solution using techniques from calculus.
Answer
The integral result is: $$ \int \frac{1}{x \sqrt{x^2 - a^2}} \, dx = \frac{1}{a} \sec^{-1}\left(\frac{x}{a}\right) + C $$
Answer for screen readers
The final result of the integral is:
$$ \int \frac{1}{x \sqrt{x^2 - a^2}} , dx = \frac{1}{a} \sec^{-1}\left(\frac{x}{a}\right) + C $$
Steps to Solve
- Rewrite the Integral Expression
We start with the integral
$$ \int \frac{1}{x \sqrt{x^2 - a^2}} , dx $$
- Substitution
Let ( x = a \sec(\theta) ). Then, the differential ( dx ) can be expressed as:
$$ dx = a \sec(\theta) \tan(\theta) , d\theta $$
The square root ( \sqrt{x^2 - a^2} ) becomes:
$$ \sqrt{a^2 \sec^2(\theta) - a^2} = a \sqrt{\sec^2(\theta) - 1} = a \tan(\theta) $$
- Change Variables in the Integral
Substituting these into the integral gives:
$$ \int \frac{1}{a \sec(\theta) \cdot a \tan(\theta)} \cdot (a \sec(\theta) \tan(\theta) , d\theta) $$
which simplifies to:
$$ \int \frac{\sec(\theta) \tan(\theta)}{a^2 \sec(\theta) \tan(\theta)} , d\theta = \int \frac{1}{a^2} , d\theta $$
- Integrate
Now we can integrate:
$$ \int \frac{1}{a^2} , d\theta = \frac{\theta}{a^2} + C $$
- Back Substitute for ( \theta )
Since we have ( \theta = \sec^{-1}\left(\frac{x}{a}\right) ), substituting back we find:
$$ \frac{\sec^{-1}\left(\frac{x}{a}\right)}{a} + C $$
Now we can rewrite this as
$$ \frac{1}{a} \sec^{-1}\left(\frac{x}{a}\right) + C $$
The final result of the integral is:
$$ \int \frac{1}{x \sqrt{x^2 - a^2}} , dx = \frac{1}{a} \sec^{-1}\left(\frac{x}{a}\right) + C $$
More Information
The integral involves a common calculus substitution method, using trigonometric identities. This process verifies that the integral given indeed equals the expression involving the secant inverse function.
Tips
- Not properly substituting for ( x ) and ( dx ), leading to incorrect integrals.
- Forgetting to handle the limits of integration properly if definite.
- Confusing secant and tangent identities.
AI-generated content may contain errors. Please verify critical information