lim (n -> ∞) (5n^3 - 6n) / (8n^4 - 3) = ?
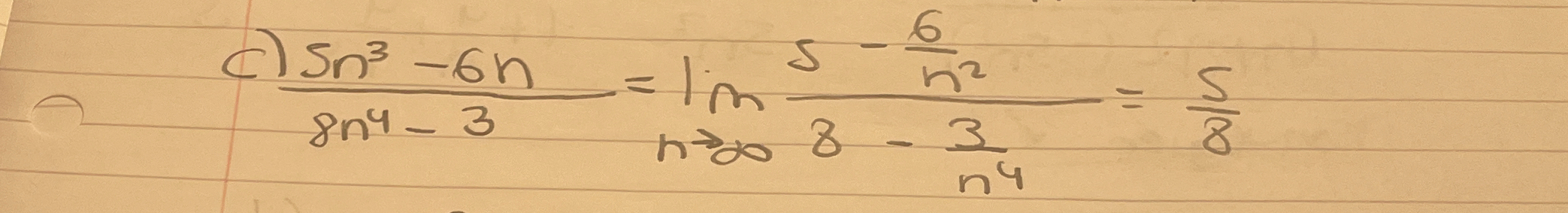
Understand the Problem
The question involves an equation relating to a limit as h approaches infinity, specifically looking at how terms behave in a rational expression.
Answer
The limit evaluates to \( \frac{5}{8} \).
Answer for screen readers
The limit is ( \frac{5}{8} ).
Steps to Solve
- Identify the limit expression
We are asked to evaluate the limit as ( h ) approaches infinity for the expression: $$ \lim_{h \to \infty} \frac{5n^3 - 6n}{8n^4 - 3} $$
- Simplify terms in the limit
As ( h ) approaches infinity, we can focus on the leading terms in both the numerator and the denominator: $$ \lim_{h \to \infty} \frac{5n^3}{8n^4} $$
- Factor out common elements
Now we divide both the numerator and the denominator by ( n^4 ) to simplify: $$ = \lim_{h \to \infty} \frac{5/n}{8} $$
- Evaluate the limit
As ( n ) approaches infinity, the term ( \frac{6}{h^2} ) approaches 0, and the term ( \frac{3}{n^4} ) also approaches 0: $$ = \frac{5}{8} $$
The limit is ( \frac{5}{8} ).
More Information
In this limit, the higher degree terms dominate both the numerator and the denominator. This means that as ( h ) goes to infinity, only the leading coefficients influence the final value.
Tips
- A common mistake is not simplifying the limit correctly by focusing on the leading terms, which can lead to incorrect results.
- Another mistake is failing to recognize that as ( n ) approaches infinity, any term divided by a higher power will approach zero.
AI-generated content may contain errors. Please verify critical information