∫ 1/√x dx
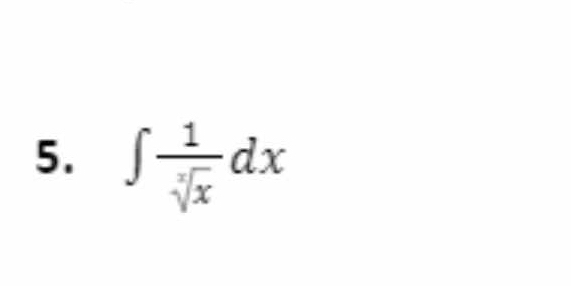
Understand the Problem
The question is asking for the evaluation of the integral of the function 1 divided by the square root of x with respect to x. This involves using integration techniques to find the antiderivative of the function.
Answer
The integral evaluates to $2\sqrt{x} + C$.
Answer for screen readers
The result of the integral is
$$ 2\sqrt{x} + C $$
Steps to Solve
- Rewrite the integral
The integral we want to evaluate is
$$ \int \frac{1}{\sqrt{x}} , dx $$
We can rewrite $\frac{1}{\sqrt{x}}$ as $x^{-1/2}$ to simplify the integration process.
- Apply the power rule for integration
Using the power rule for integration, which states that
$$ \int x^n , dx = \frac{x^{n+1}}{n+1} + C $$
for $n \neq -1$, we set $n = -\frac{1}{2}$.
- Calculate the antiderivative
Following the power rule, we get:
$$ \int x^{-1/2} , dx = \frac{x^{(-1/2) + 1}}{(-1/2) + 1} + C $$
This simplifies to:
$$ = \frac{x^{1/2}}{1/2} + C = 2\sqrt{x} + C $$
- Final result
Thus, the antiderivative of the original integral is:
$$ \int \frac{1}{\sqrt{x}} , dx = 2\sqrt{x} + C $$
where $C$ is the constant of integration.
The result of the integral is
$$ 2\sqrt{x} + C $$
More Information
This integral is a common example in calculus for introducing the power rule. The function $\frac{1}{\sqrt{x}}$ is particularly important in applications related to area under curves and rates of change.
Tips
- Forgetting to use the power rule and attempting to evaluate the integral without rewriting the integrand.
- Neglecting to add the constant of integration $C$ after integration.
AI-generated content may contain errors. Please verify critical information