∫ 1/√x dx
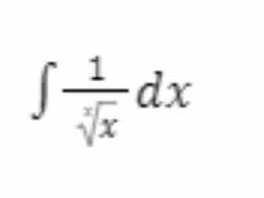
Understand the Problem
The question is asking us to solve the integral of the function 1/√x with respect to x. This involves applying integral calculus techniques to find the antiderivative of the given function.
Answer
$$ 2\sqrt{x} + C $$
Answer for screen readers
The integral of ( \frac{1}{\sqrt{x}} ) with respect to ( x ) is:
$$ 2\sqrt{x} + C $$
Steps to Solve
- Rewrite the integral in exponent form
The function ( \frac{1}{\sqrt{x}} ) can be rewritten as ( x^{-\frac{1}{2}} ).
Thus, the integral becomes:
$$ \int x^{-\frac{1}{2}} , dx $$
- Apply the power rule for integration
The power rule states that:
$$ \int x^n , dx = \frac{x^{n+1}}{n+1} + C $$
where ( n \neq -1 ). Here, ( n = -\frac{1}{2} ), so:
$$ n + 1 = -\frac{1}{2} + 1 = \frac{1}{2} $$
- Integrate using the power rule
Now apply the power rule:
$$ \int x^{-\frac{1}{2}} , dx = \frac{x^{\frac{1}{2}}}{\frac{1}{2}} + C $$
Which simplifies to:
$$ 2x^{\frac{1}{2}} + C $$
- Rewrite in terms of the square root
Since ( x^{\frac{1}{2}} ) is the same as ( \sqrt{x} ), we can write:
$$ 2\sqrt{x} + C $$
The integral of ( \frac{1}{\sqrt{x}} ) with respect to ( x ) is:
$$ 2\sqrt{x} + C $$
More Information
This integral is a fundamental result in calculus, often encountered when working with power functions. The constant ( C ) represents the constant of integration, which appears because indefinite integrals can have infinitely many solutions differing by a constant.
Tips
- Forgetting to add the constant ( C ) after integrating.
- Misapplying the power rule when calculating the new exponent and denominator.