√172 - √252
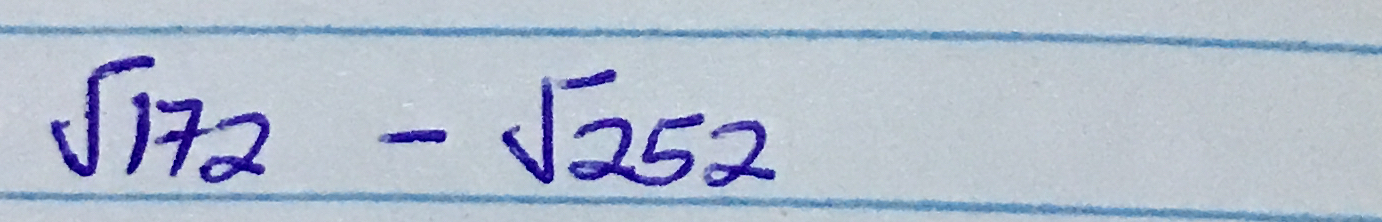
Understand the Problem
The question is asking us to simplify the expression given, which involves finding the square roots of 172 and 252, and then performing the subtraction. This requires the application of basic algebraic principles.
Answer
The simplified expression is $2(\sqrt{43} - 3\sqrt{7})$.
Answer for screen readers
The simplified expression is $2(\sqrt{43} - 3\sqrt{7})$.
Steps to Solve
- Simplifying the square roots
First, we need to simplify both square roots.
For $\sqrt{172}$, we can factor it:
$$ 172 = 4 \times 43 $$
So,
$$ \sqrt{172} = \sqrt{4 \times 43} = \sqrt{4} \times \sqrt{43} = 2\sqrt{43} $$
Next, for $\sqrt{252}$, we can factor it:
$$ 252 = 4 \times 63 $$
This gives us:
$$ \sqrt{252} = \sqrt{4 \times 63} = \sqrt{4} \times \sqrt{63} = 2\sqrt{63} $$
- Further simplify $\sqrt{63}$
Now, we can simplify $\sqrt{63}$ further:
$$ 63 = 9 \times 7 $$
Thus,
$$ \sqrt{63} = \sqrt{9 \times 7} = \sqrt{9} \times \sqrt{7} = 3\sqrt{7} $$
- Substituting the simplified values
Now substitute the simplified square roots back into the original expression:
$$ \sqrt{172} - \sqrt{252} = 2\sqrt{43} - 2\sqrt{63} = 2(\sqrt{43} - 3\sqrt{7}) $$
- Final expression
So, the final simplified form of the expression is:
$$ 2(\sqrt{43} - 3\sqrt{7}) $$
The simplified expression is $2(\sqrt{43} - 3\sqrt{7})$.
More Information
The square roots were simplified by factoring out perfect squares and using the property $\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}$. The process led to a clearer expression that showcases the relationship between the numbers.
Tips
- Not factoring correctly: Ensure to find the correct perfect squares when simplifying square roots.
- Forgetting to distribute: When substituting back, remember to factor completely and simplify properly.
AI-generated content may contain errors. Please verify critical information