16. 3^3 + 5 × 3 _____ 2 + 8(35 ÷ 7) 17. 8 × (-2) - (-4)² _____ 34 ÷ 9 + 2 × 5 18. 5 × 2² - 2³(-6+3) _____ 6(2 + 9) - 3³ ÷ 9 - 4
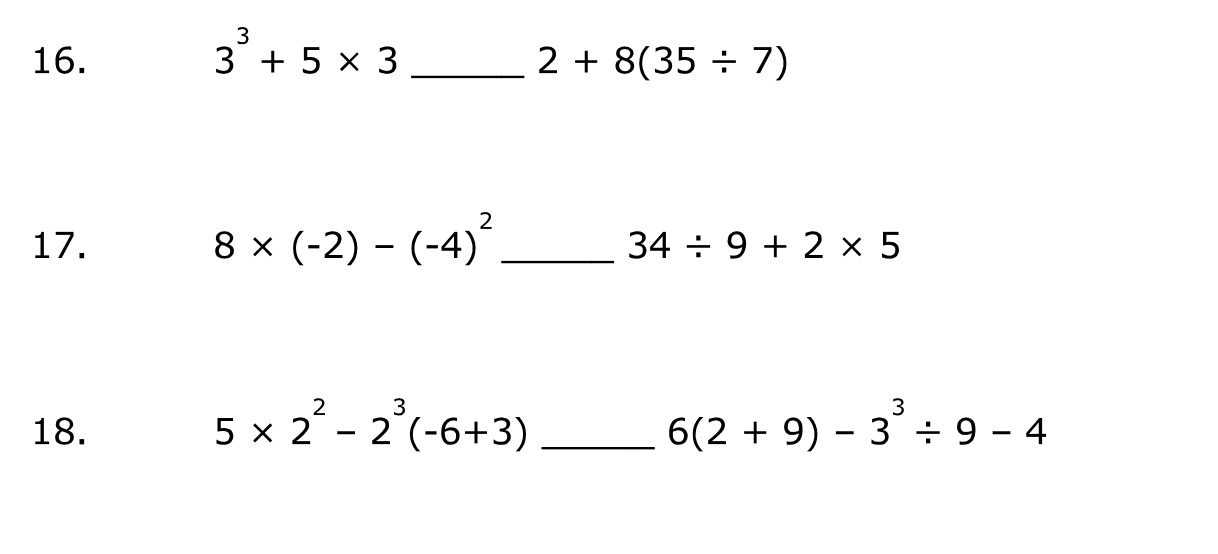
Understand the Problem
The question involves solving three mathematical expressions with various operations such as addition, multiplication, exponentiation, and division. Each expression contains a blank where the user needs to determine the correct mathematical operator.
Answer
16. = 17. < 18. <
Answer for screen readers
- =
- <
- <
Steps to Solve
-
Evaluate Expression Step by Step
First, we evaluate the left side of each expression. For each equation, we apply the order of operations (PEMDAS/BODMAS).
Expression 16:
Evaluate $3^3 + 5 \times 3$:
$$ 3^3 = 27 $$
$$ 5 \times 3 = 15 $$
So, $27 + 15 = 42$. Now calculate the right side:
$$ 35 \div 7 = 5 $$
Thus, the expression becomes:
$$ 42 , ? , 2 + 8 \times 5 $$
Expression 17:
Calculate left side:
$$ 8 \times (-2) - (-4)^2 = -16 - 16 = -32 $$
Now calculate the right side:
$$ 34 \div 9 + 2 \times 5 = \frac{34}{9} + 10 $$
Expression 18:
Evaluate left side:
$$ 5 \times 2^2 - 2^3(-6 + 3) = 5 \times 4 - 8 \times -3 = 20 + 24 = 44 $$
For the right side:
$$ 6(2 + 9) - 3^3 \div 9 - 4 = 6 \times 11 - \frac{27}{9} - 4 = 66 - 3 - 4 = 59 $$
-
Determine the Operators
Next, we need to establish the operators needed in each expression to maintain equality.
Expression 16:
Now compare:
$$ 42 , ? , 2 + 40 $$
$$ 42 , ? , 42 $$
We see that $42 = 42$, thus the operator is $=$.
Expression 17:
Compare:
$$ -32 , ? , \frac{34}{9} + 10 $$
$$ -32 , ? , > , \left(\frac{34}{9} + 10\right) $$
Since the right side is greater, the operator is $<$.
Expression 18:
Comparing:
$$ 44 , ? , 59 $$
$$ 44 < 59 $$
So the operator is $<$.
- =
- <
- <
More Information
In these expressions, the process of evaluation followed the standard mathematical rules. Each statement was reasoned based on the calculated outcomes from both sides of the equations.
Tips
- Failing to follow the order of operations (PEMDAS/BODMAS) can lead to incorrect evaluations of the expressions.
- Not simplifying fractions properly can also cause errors in comparisons.
AI-generated content may contain errors. Please verify critical information