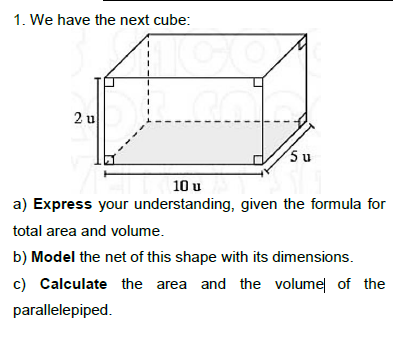
1. We have the next cube: a) Express your understanding, given the formula for total area and volume. b) Model the net of this shape with its dimensions. c) Calculate the area and... 1. We have the next cube: a) Express your understanding, given the formula for total area and volume. b) Model the net of this shape with its dimensions. c) Calculate the area and the volume of the parallelepiped.
Understand the Problem
The question is asking to express the formulas for total area and volume of a cube, model its net with dimensions, and calculate both the area and volume of the parallelepiped. This involves applying geometric formulas and creating a visual representation.
Answer
Total Surface Area: $A = 160u^2$, Volume: $V = 100u^3$.
Answer for screen readers
The total surface area of the parallelepiped is $A = 160u^2$ and the volume is $V = 100u^3$.
Steps to Solve
- Identify the dimensions of the parallelepiped
The dimensions given are:
- Length (l) = $10u$
- Width (w) = $5u$
- Height (h) = $2u$
- Write the formulas for total surface area and volume
The formulas are:
- Total Surface Area (A) of a parallelepiped is given by:
$$ A = 2(lw + lh + wh) $$ - Volume (V) of a parallelepiped is given by:
$$ V = l \times w \times h $$
- Plug in the dimensions to calculate total surface area
Substituting values into the surface area formula:
$$ A = 2(10u \cdot 5u + 10u \cdot 2u + 5u \cdot 2u) $$
Calculating each term:
- $lw = 10u \cdot 5u = 50u^2$
- $lh = 10u \cdot 2u = 20u^2$
- $wh = 5u \cdot 2u = 10u^2$
Now substituting these values into the area formula:
$$ A = 2(50u^2 + 20u^2 + 10u^2) $$
$$ A = 2(80u^2) $$
$$ A = 160u^2 $$
- Plug in the dimensions to calculate the volume
Substituting values into the volume formula:
$$ V = 10u \cdot 5u \cdot 2u $$
Calculating the volume:
$$ V = 100u^3 $$
- Model the Net of the Parallelepiped
To model the net of the parallelepiped, draw the six faces:
- Two rectangles of dimension $10u \times 5u$ (front and back)
- Two rectangles of dimension $10u \times 2u$ (top and bottom)
- Two rectangles of dimension $5u \times 2u$ (left and right sides)
Label each rectangle with its dimensions.
The total surface area of the parallelepiped is $A = 160u^2$ and the volume is $V = 100u^3$.
More Information
The total surface area accounts for all the outer surfaces of the parallelepiped, while the volume represents the space contained within it. Understanding how to compute these measurements is vital in geometry, especially for practical applications like packaging and construction.
Tips
- Forgetting to multiply by 2 for the surface area calculation, as it includes both pairs of opposite faces.
- Mixing up the dimensions when substituting into the formulas, which can lead to incorrect answers.