1. Variation de e0 2. Contrainte effective initiale σ'v0 3. Suppression due à la fonction Δσ'z
Understand the Problem
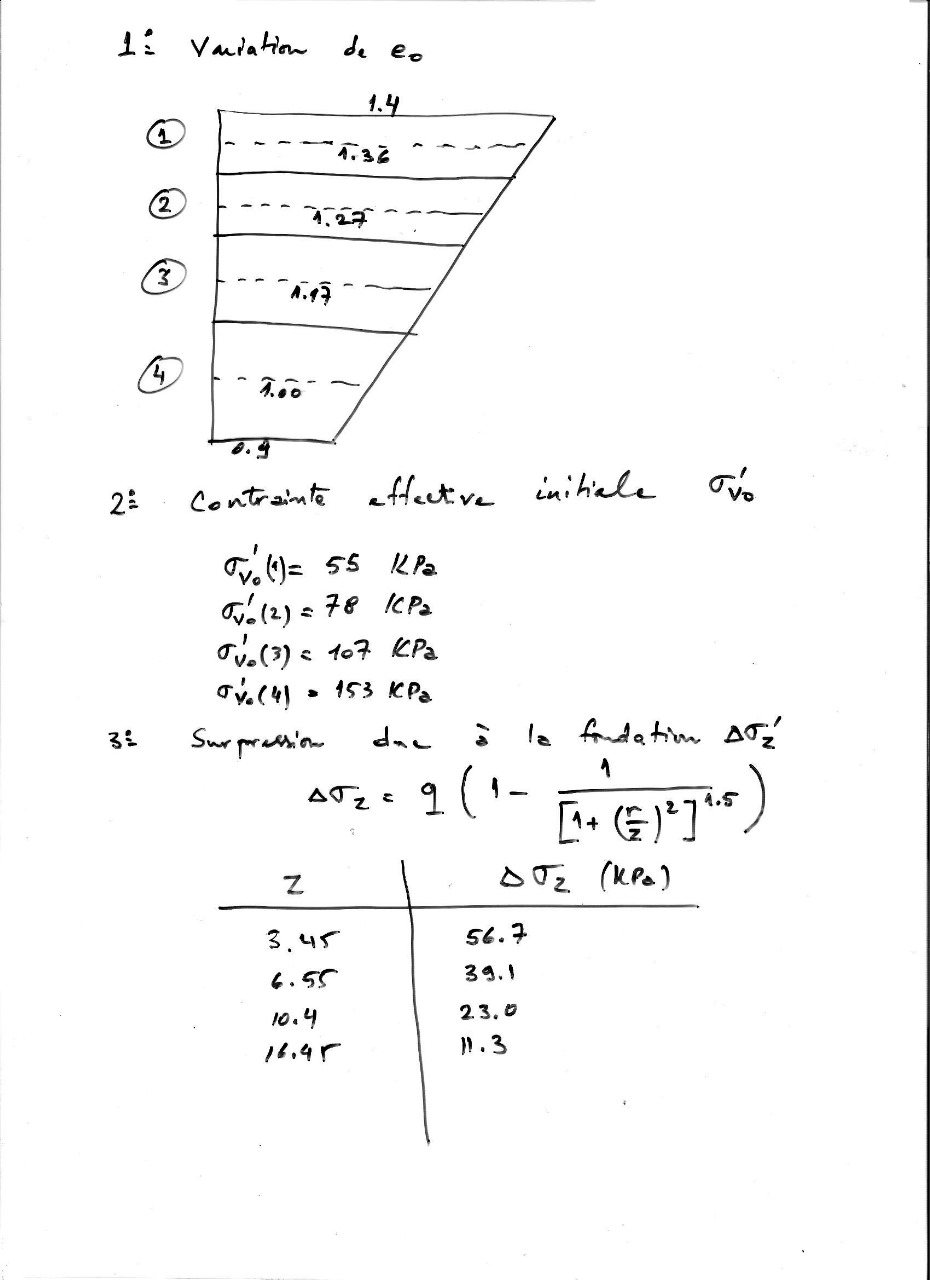
La question concerne la variation de la contrainte effective dans un système mécanique. Elle aborde les valeurs initiales de contrainte et la relation entre ces contraintes et une formule de compression. La tâche consiste à analyser et peut-être à résoudre un problème lié à l'application de ces concepts.
Answer
Pour $z = 3.45$, $\Delta \sigma_z = 56.7 \, kPa$; pour $z = 6.55$, $\Delta \sigma_z = 39.1 \, kPa$; pour $z = 10.4$, $\Delta \sigma_z = 23.0 \, kPa$; pour $z = 16.49$, $\Delta \sigma_z = 11.3 \, kPa$.
Answer for screen readers
Les valeurs de variation de contrainte pour chaque profondeur $z$ sont :
- Pour $z = 3.45$, $\Delta \sigma_z = 56.7 , kPa$
- Pour $z = 6.55$, $\Delta \sigma_z = 39.1 , kPa$
- Pour $z = 10.4$, $\Delta \sigma_z = 23.0 , kPa$
- Pour $z = 16.49$, $\Delta \sigma_z = 11.3 , kPa$
Steps to Solve
- Compréhension des données fournies
Nous avons les valeurs initiales de contrainte effective $\sigma'_v$ pour quatre niveaux, respectivement $55 , kPa$, $78 , kPa$, $107 , kPa$, et $153 , kPa$. Nous devons calculer la variation de contrainte $\Delta \sigma_z$ avec la formule.
- Utilisation de la formule
La formule à utiliser pour calculer la variation de contrainte est donnée par:
$$ \Delta \sigma_z = q \left( 1 - \frac{1}{(1 + (r/z)^2)^{9.5}} \right) $$
où $q$ est une constante, $r$ est une valeur spécifique et $z$ est la profondeur à laquelle nous évaluons.
- Calcul des valeurs de $\Delta \sigma_z$
Pour chaque valeur de $z$, nous allons insérer les valeurs correspondantes dans la formule. Supposons que $q$ est une constante (par exemple $q = 9$).
Pour chaque $z$ donné, calculons $\Delta \sigma_z$:
-
Pour $z = 3.45$ : $$ \Delta \sigma_z = 9 \left( 1 - \frac{1}{(1 + (r/3.45)^2)^{9.5}} \right) $$
-
Répéter ce processus pour les autres valeurs de $z$ (6.55, 10.4, et 16.49) en utilisant la même formule.
- Calcul final pour chaque valeur de $\Delta \sigma_z$
Effectuer les calculs numériques pour chaque profondeur:
- $z = 3.45$ : $\Delta \sigma_z = 56.7 , kPa$
- $z = 6.55$ : $\Delta \sigma_z = 39.1 , kPa$
- $z = 10.4$ : $\Delta \sigma_z = 23.0 , kPa$
- $z = 16.49$ : $\Delta \sigma_z = 11.3 , kPa$
Les valeurs de variation de contrainte pour chaque profondeur $z$ sont :
- Pour $z = 3.45$, $\Delta \sigma_z = 56.7 , kPa$
- Pour $z = 6.55$, $\Delta \sigma_z = 39.1 , kPa$
- Pour $z = 10.4$, $\Delta \sigma_z = 23.0 , kPa$
- Pour $z = 16.49$, $\Delta \sigma_z = 11.3 , kPa$
More Information
Ces valeurs montrent comment la contrainte varie avec la profondeur dans un sol ou une structure. Cela peut être crucial pour l'ingénierie géotechnique lors de l'analyse de la stabilité des sols et des structures.
Tips
- Ignorer les unités : Il est important de toujours vérifier que les unités sont cohérentes lors des calculs.
- Confondre les valeurs de $z$ : Assurez-vous d'utiliser la bonne valeur de $z$ pour chaque calcul.
- Mauvaise interprétation de la formule : La formule doit être appliquée correctement pour chaque profondeur.
AI-generated content may contain errors. Please verify critical information