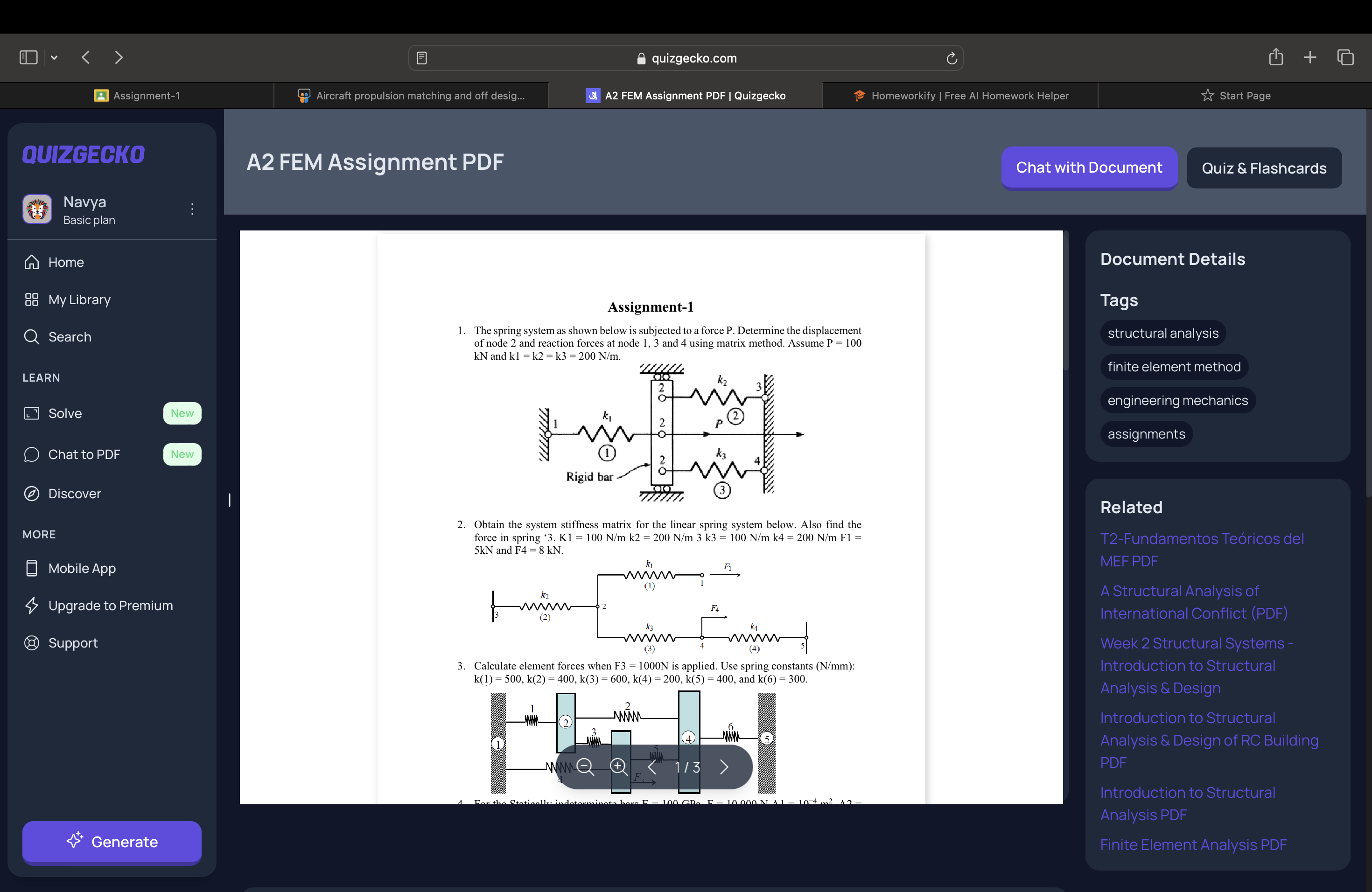
1. The spring system shown is subjected to a force P = 100 kN. Determine the displacement of node 2 and reaction forces at node 1, 3, and 4 using matrix method. k1 = k2 = k3 = 200... 1. The spring system shown is subjected to a force P = 100 kN. Determine the displacement of node 2 and reaction forces at node 1, 3, and 4 using matrix method. k1 = k2 = k3 = 200 Nm. 2. Obtain the system stiffness matrix for the linear spring system and find the force in spring 3. 3. Calculate element forces when F3 = 1000 N is applied with given spring constants. 4. For the stability in determining force F = 1000 N, A1 = 10^-6 m^2, A2 = 0.5 A1, and E1 = 200 Gpa; calculate.
Understand the Problem
The question is asking about performing calculations related to a spring system subjected to forces using the finite element method and matrix analysis. It involves determining displacements, reaction forces, and creating a stiffness matrix for the system.
Answer
The displacement of node 2 ($u_2$) and reaction forces must be calculated using the stiffness matrix and displacement equations.
Answer for screen readers
The displacement of node 2 is $u_2$ and the reaction forces at node 1 are determined from the calculated displacements.
Steps to Solve
-
Determine the stiffness values for each spring Given the spring constants:
- $k_1 = k_2 = k_3 = 200 , \text{N/m}$
- $k_4 = 100 , \text{N/m}$
-
Set up the system of equations Using the finite element method, we can derive the stiffness matrix, which relates the displacements to the forces. For three springs and known forces: $$ \begin{bmatrix} k_1 + k_2 & -k_2 \ -k_2 & k_2 + k_3 \end{bmatrix} \begin{bmatrix} u_1 \ u_2 \end{bmatrix}
\begin{bmatrix} F_1 \ F_2 \end{bmatrix} $$
-
Write the force vector In this case, the only external force involved is $P = 100 , \text{kN}$. The force vector can be adjusted based on how the displacements and forces are applied to the nodes.
-
Calculate the displacement vector Solve the system of equations for the displacement vector: $$ \begin{bmatrix} u_1 \ u_2 \end{bmatrix} = K^{-1} F $$
-
Substitute known values and solve Substitute the values of the stiffness matrix $K$ and the forces $F$ into the equation and solve for the displacements $u_1$ and $u_2$.
-
Determine reaction forces Once the displacements are known, calculate the reaction forces at the nodes using the relationship: $$ F = k \cdot u $$
The displacement of node 2 is $u_2$ and the reaction forces at node 1 are determined from the calculated displacements.
More Information
In structural analysis, understanding how to calculate displacements and reactions in a spring system is crucial for ensuring stability and integrity in engineering structures.
Tips
- Incorrect assembly of the stiffness matrix, which may lead to erroneous results.
- Failing to account for all forces applied to the system, which can result in incorrect displacement values.
AI-generated content may contain errors. Please verify critical information