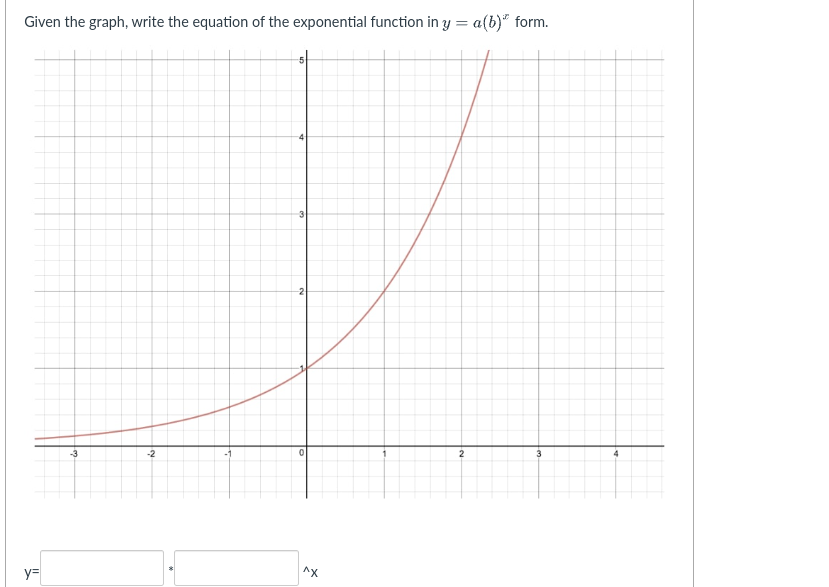
Given the graph, write the equation of the exponential function in y = a(b)^x form.
Understand the Problem
The question is asking for the equation of an exponential function based on the provided graph, specifically in the form y = a(b)^x.
Answer
The equation of the exponential function is \(y = 2^x\).
Answer for screen readers
The equation of the exponential function is (y = 2^x).
Steps to Solve
- Identify Key Points on the Graph
To write the equation in the form (y = a(b)^x), we need to identify points on the graph. Common points to check are (0, 1) and (1, b) where the value of (b) is determined by the graph.
- Find the Value of (a)
The value (a) represents the y-intercept, which is the value of (y) when (x = 0). From the graph, (y = a(1)^0 = a). If (y = 1) when (x = 0), then (a = 1).
- Determine the Value of (b)
To find (b), look for another point on the graph, for instance, (1, 2). If (x = 1) yields (y = 2), we substitute into the equation: $$ 2 = a(b)^1 $$ Given (a = 1): $$ 2 = 1 \cdot b \implies b = 2 $$
- Write the Final Equation
Now that we have (a) and (b), we can write the equation of the exponential function: $$ y = 1(2)^x $$ This simplifies to: $$ y = 2^x $$
The equation of the exponential function is (y = 2^x).
More Information
Exponential functions are a fundamental concept in math, often describing growth or decay processes in real-world applications such as population growth, radioactive decay, and finance.
Tips
- A common mistake is misreading the graph and incorrectly identifying points. Always double-check the coordinates.
- Another mistake is forgetting that (a) is the y-intercept; ensure proper evaluation of the function at (x = 0).
AI-generated content may contain errors. Please verify critical information