1 - Résoudre les équations suivantes : a - 7√3x - √3 = 0 b - x + √8 = 3x c - 3x - 8/3 = x - 7(x - 1) 2 - Soit x un nombre réel. a) Vérifier que : 6x² + 11x - 2 = (6x - 1)(x + 2) b)... 1 - Résoudre les équations suivantes : a - 7√3x - √3 = 0 b - x + √8 = 3x c - 3x - 8/3 = x - 7(x - 1) 2 - Soit x un nombre réel. a) Vérifier que : 6x² + 11x - 2 = (6x - 1)(x + 2) b) Dédire la résolution de l'équation : 6x² + 11x = 2
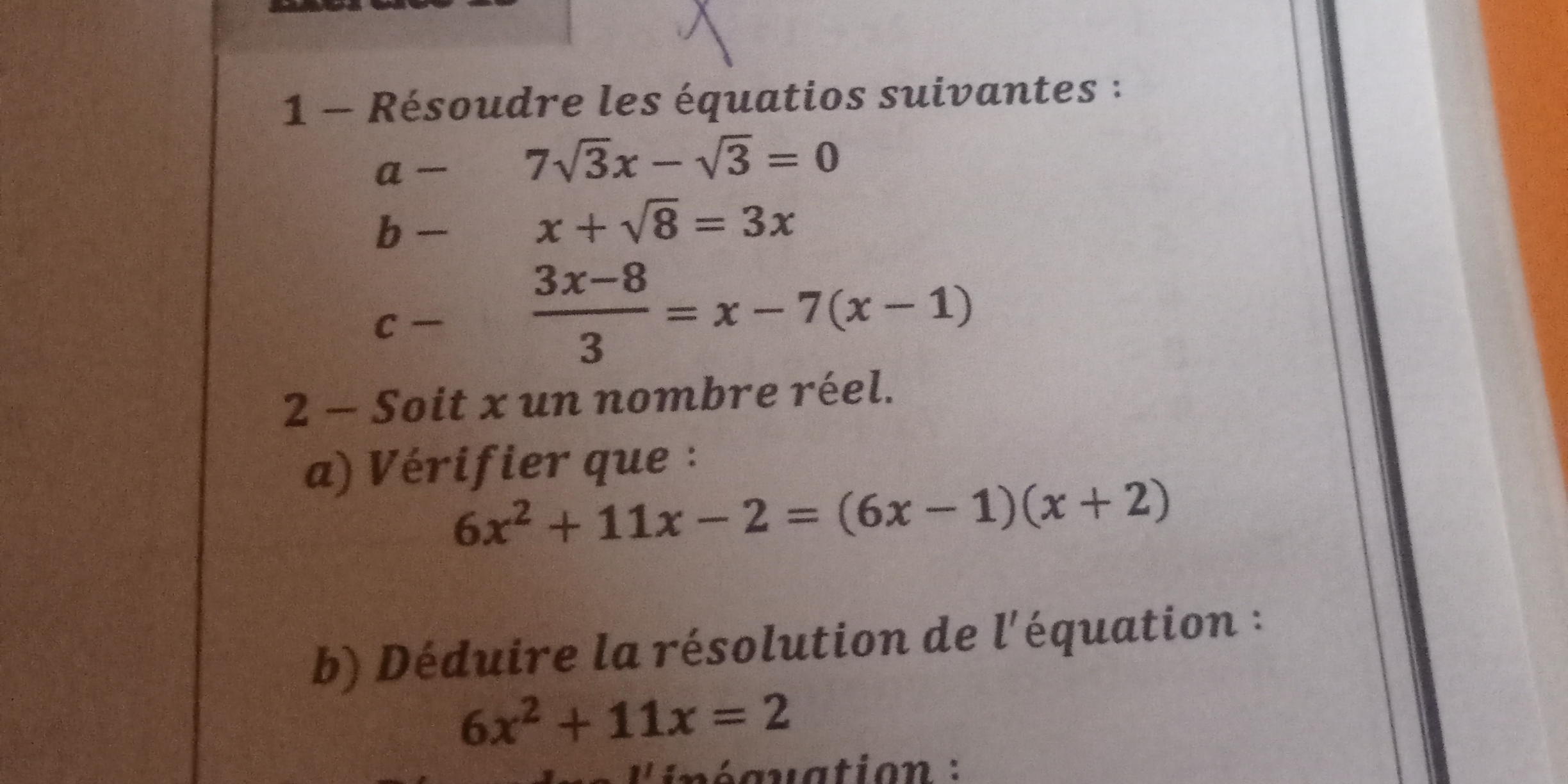
Understand the Problem
La question demande de résoudre plusieurs équations et de vérifier une relation algébrique. Ça implique des étapes de simplification et de calcul, ce qui requiert une compréhension des algèbres et des équations.
Answer
Les solutions sont : $x = -\frac{1}{7}$, $x = \sqrt{2}$, $x = \frac{13}{7}$, et les solutions de $6x^2 + 11x - 2 = 0$ sont $x = \frac{1}{6}$ et $x = -2$.
Answer for screen readers
Les solutions sont :
a) $x = -\frac{1}{7}$
b) $x = \sqrt{2}$
c) $x = \frac{13}{7}$
Les solutions de l'équation $6x^2 + 11x - 2 = 0$ sont : $x = \frac{1}{6}$ et $x = -2$.
Steps to Solve
-
Résoudre l'équation a
L'équation est :
$$ -7\sqrt{3}x - \sqrt{3} = 0 $$
Ajoutons $\sqrt{3}$ des deux côtés :
$$ -7\sqrt{3}x = \sqrt{3} $$
Divisons par $-7\sqrt{3}$ :
$$ x = -\frac{1}{7} $$ -
Résoudre l'équation b
L'équation est :
$$ x + \sqrt{8} = 3x $$
Soustrayons $x$ des deux côtés :
$$ \sqrt{8} = 2x $$
Divisons par 2 :
$$ x = \frac{\sqrt{8}}{2} = \sqrt{2} $$ -
Résoudre l'équation c
L'équation est :
$$ \frac{3x - 8}{3} = x - 7(x - 1) $$
Multipliant tout par 3 :
$$ 3x - 8 = 3x - 21 + 7x $$
Simplifions :
$$ -8 = -21 + 7x $$
Ajoutons 21 aux deux côtés :
$$ 13 = 7x $$
Divisons par 7 :
$$ x = \frac{13}{7} $$ -
Vérifier l'égalité (a)
Nous devons vérifier que :
$$ 6x^2 + 11x - 2 = (6x - 1)(x + 2) $$
Développons le côté droit :
$$ (6x - 1)(x + 2) = 6x^2 + 12x - x - 2 = 6x^2 + 11x - 2 $$
Ainsi, l'égalité est vérifiée. -
Déduire la résolution de l'équation (b)
L'équation à résoudre est :
$$ 6x^2 + 11x = 2 $$
En réorganisant, nous obtenons :
$$ 6x^2 + 11x - 2 = 0 $$
Cela correspond à l'équation vérifiée précédemment. Utilisons la méthode du discriminant :
$$ \Delta = b^2 - 4ac = 11^2 - 4 \times 6 \times (-2) = 121 + 48 = 169 $$
Comme $\Delta > 0$, il y a deux solutions :
$$ x = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-11 \pm 13}{12}$$
Résolvons les deux cas :
$$ x_1 = \frac{2}{12} = \frac{1}{6}, \quad x_2 = \frac{-24}{12} = -2 $$
Les solutions sont :
a) $x = -\frac{1}{7}$
b) $x = \sqrt{2}$
c) $x = \frac{13}{7}$
Les solutions de l'équation $6x^2 + 11x - 2 = 0$ sont : $x = \frac{1}{6}$ et $x = -2$.
More Information
Cela montre l'importance de la factorisation et de l'utilisation du discriminant pour résoudre les équations quadratiques. La vérification d'une égalité algébrique renforce la compréhension des propriétés des équations.
Tips
- Ne pas isoler correctement les termes dans les équations.
- Oublier de vérifier les solutions dans le contexte de l'équation initiale après les avoir trouvées.
AI-generated content may contain errors. Please verify critical information