1. Find the Taylor's series expansion of: f(x, y) = x^3 + xy^2 about point (2, 1). 2. Find the first six terms of the expansions of the function e^x log(1 + y) in a neighbourhood o... 1. Find the Taylor's series expansion of: f(x, y) = x^3 + xy^2 about point (2, 1). 2. Find the first six terms of the expansions of the function e^x log(1 + y) in a neighbourhood of the point (0, 0). 3. Prove that a^x = 1 + x log a + (x^2/(2!))(log a)^2 + (x^2/(3!))(log a)^3 + …… 4. Expand x^2y + 3y - 2 in powers of (x - 1) and (y + 2) using Taylor's Theorem. 5. Expand x^y in powers of (x - 1) and (y - 1) up to the third-degree terms and percentage change in the volume of the balloon.
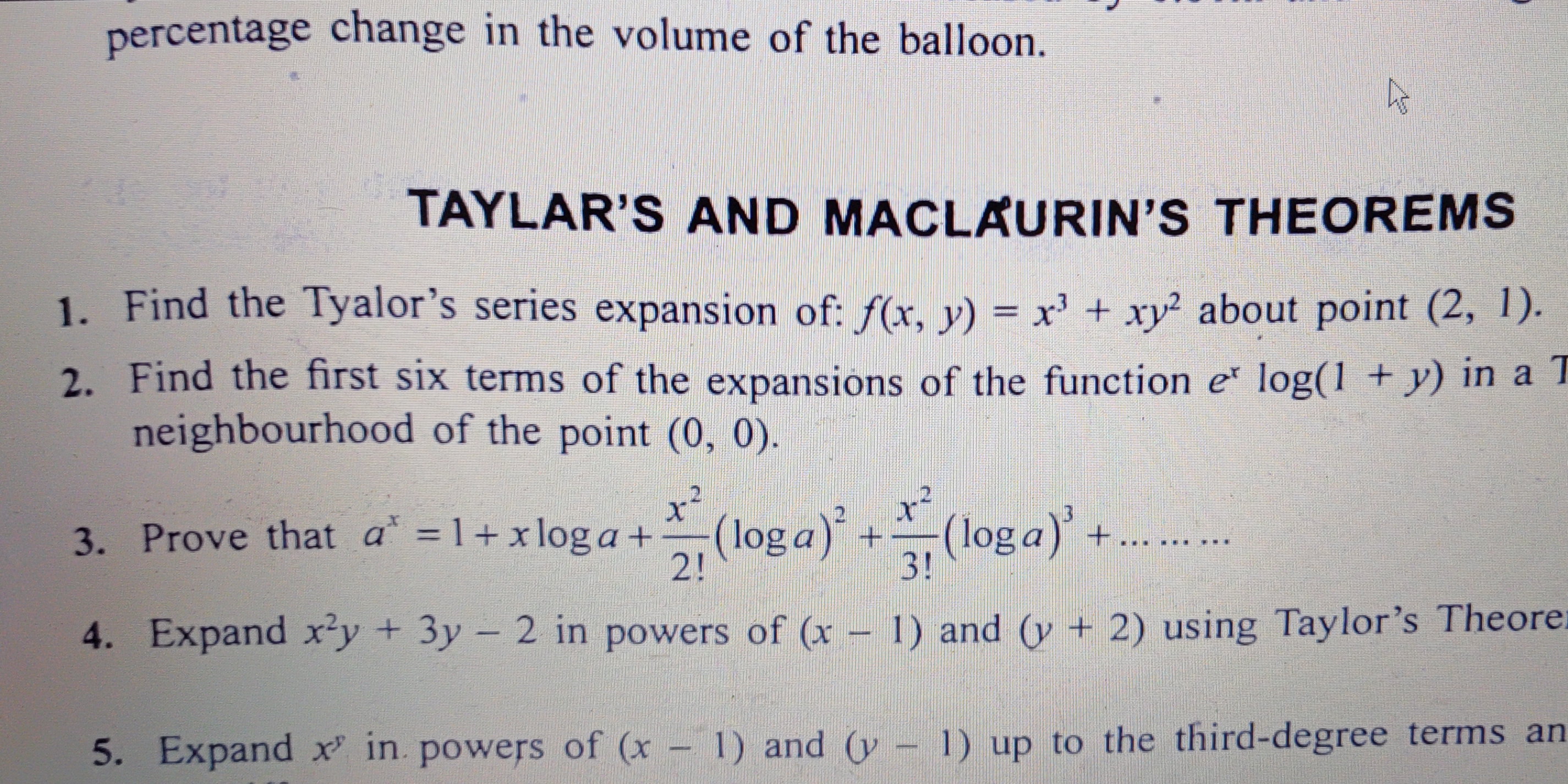
Understand the Problem
The question is asking to apply Taylor's and Maclaurin's Theorems to find series expansions and terms for given mathematical functions, which involves calculus techniques for approximation of functions.
Answer
The Taylor series expansion is $$ f(x,y) \approx 10 + 13(x-2) + 4(y-1) + 6(x-2)^2 + (y-1)^2 + 2(x-2)(y-1) $$
Answer for screen readers
The Taylor series expansion of ( f(x, y) = x^3 + xy^2 ) about ( (2, 1) ) is:
$$ f(x, y) \approx 10 + 13(x-2) + 4(y-1) + 6(x-2)^2 + (y-1)^2 + 2(x-2)(y-1) $$
The first six terms of the expansion of ( e^x \log(1 + y) ) need computation of derivatives.
Steps to Solve
- Taylor's Series Expansion of ( f(x, y) = x^3 + xy^2 )
To find the Taylor's series expansion of ( f(x, y) ) about the point ( (2, 1) ), we need to calculate the function's value, and its first few partial derivatives at that point.
Calculate ( f(2, 1) = 2^3 + 2(1^2) = 8 + 2 = 10 ).
Next, find the first-order partial derivatives:
- ( f_x(x, y) = 3x^2 + y^2 )
- ( f_y(x, y) = 2xy )
At ( (2, 1) ):
- ( f_x(2, 1) = 3(2^2) + 1^2 = 12 + 1 = 13 )
- ( f_y(2, 1) = 2(2)(1) = 4 )
Now, find the second-order derivatives:
- ( f_{xx}(x, y) = 6x )
- ( f_{yy}(x, y) = 2x )
- ( f_{xy}(x, y) = 2y )
At ( (2, 1) ):
- ( f_{xx}(2, 1) = 12 )
- ( f_{yy}(2, 1) = 4 )
- ( f_{xy}(2, 1) = 2 )
Using these values, we can write the Taylor series:
[ f(x, y) \approx f(2, 1) + f_x(2, 1)(x - 2) + f_y(2, 1)(y - 1) + \frac{1}{2!} f_{xx}(2, 1)(x - 2)^2 + \frac{1}{2!} f_{yy}(2, 1)(y - 1)^2 + f_{xy}(2, 1)(x - 2)(y - 1) ]
- Expanding the Series
Substituting the values into the Taylor series formula:
[ f(x, y) \approx 10 + 13(x - 2) + 4(y - 1) + \frac{12}{2}(x - 2)^2 + 2(y - 1)^2 + 2(x - 2)(y - 1) ]
Simplifying this gives the expansion around ( (2, 1) ).
- Finding the first six terms of ( e^x \log(1 + y) )
The function is ( h(x, y) = e^x \log(1 + y) ).
Calculate ( h(0, 0) = e^0 \log(1 + 0) = 0 ).
Find first-order derivatives:
- ( h_x = e^x \log(1 + y) )
- ( h_y = \frac{e^x}{1 + y} )
Evaluate at ( (0, 0) ):
- ( h_x(0, 0) = 1 \cdot 0 = 0 )
- ( h_y(0, 0) = 1 )
Continuing this process to get higher-order derivatives and their evaluations would yield the coefficients for the expansion, leading to the first six terms.
- Proof of ( a^x )
To show ( a^x = 1 + x \log a + \frac{x^2}{2!} (\log a)^2 + \frac{x^3}{3!} (\log a)^3 + \dots ), we expand ( e^{x \log a} ) using the Taylor series around ( x = 0 ).
- Power Series Expansion of ( x^2y + 3y - 2 )
Using ( x - 1 ) and ( y + 2 ) as the variables and applying Taylor's theorem would give the required expansion, collecting terms in powers of ( (x - 1) ) and ( (y + 2) ).
- Expansion of ( x^y )
Using Taylor expansion gives ( x^y ) in terms of ( (x - 1) ) and ( (y - 1) ), retaining terms up to the third degree.
The Taylor series expansion of ( f(x, y) = x^3 + xy^2 ) about ( (2, 1) ) is:
$$ f(x, y) \approx 10 + 13(x-2) + 4(y-1) + 6(x-2)^2 + (y-1)^2 + 2(x-2)(y-1) $$
The first six terms of the expansion of ( e^x \log(1 + y) ) need computation of derivatives.
More Information
Taylor and Maclaurin's theorems allow functions to be approximated by polynomials. The approximation can be essential in calculus and analytical computations.
Tips
- Not evaluating the function and derivatives at the correct point.
- Forgetting to account for higher-order terms in the series.
- Mixing up variables during partial differentiation.
AI-generated content may contain errors. Please verify critical information