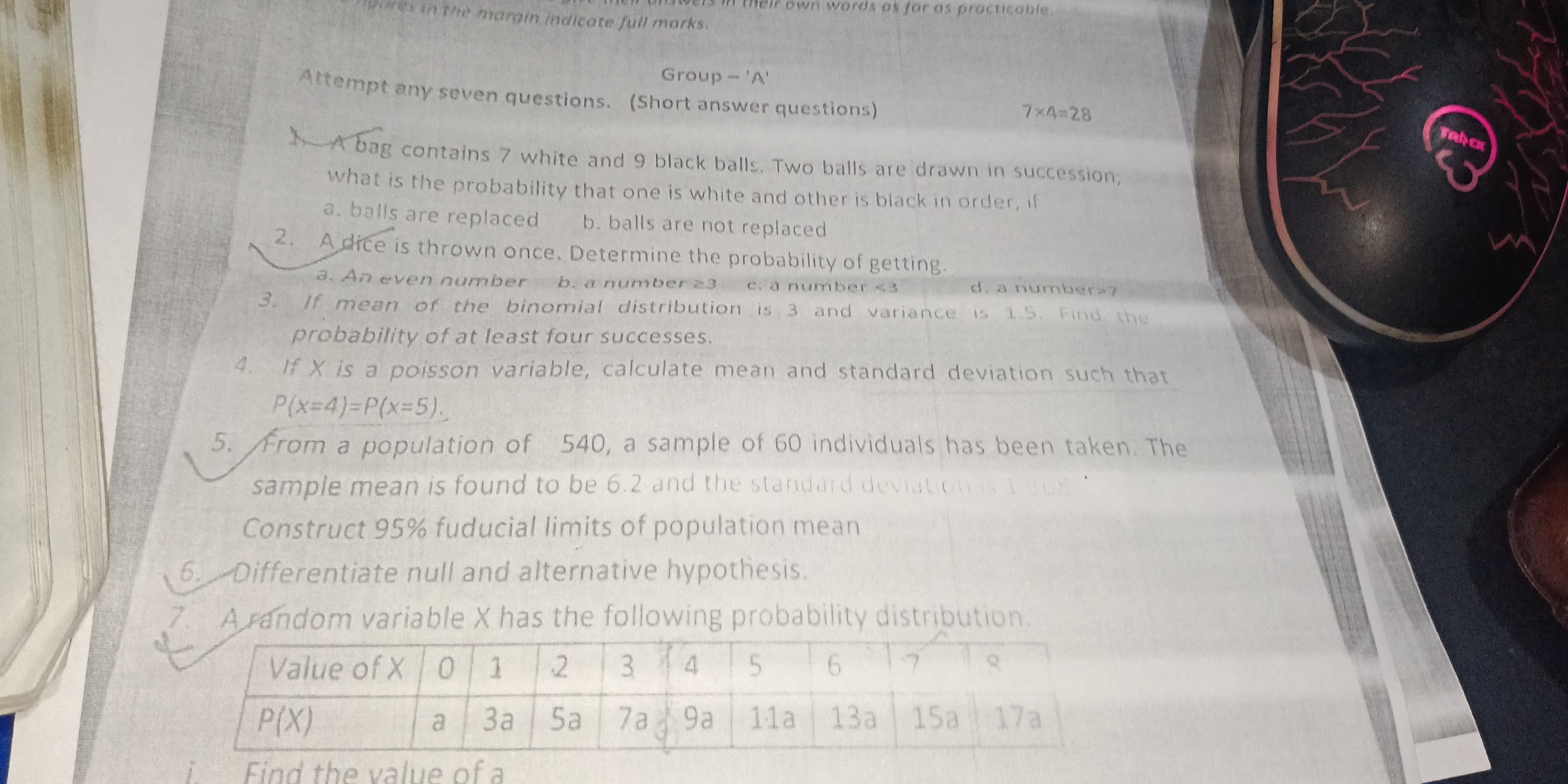
1. A bag contains 7 white and 9 black balls. Two balls are drawn in succession. What is the probability that one is white and the other is black in order, if: a. balls are replaced... 1. A bag contains 7 white and 9 black balls. Two balls are drawn in succession. What is the probability that one is white and the other is black in order, if: a. balls are replaced b. balls are not replaced? 2. A dice is thrown once. Determine the probability of getting: a. an even number b. a number ≤ 3 c. a number < 3 d. a number ≥ 7. 3. If the mean of the binomial distribution is 3 and variance is 1.5, find the probability of at least four successes. 4. If X is a Poisson variable, calculate mean and standard deviation such that P(X=4)=P(X=5). 5. From a population of 540, a sample of 60 individuals has been taken. The sample mean is found to be 6.2 and the standard deviation is 1.3. Construct 95% fiducial limits of population mean. 6. Differentiate null and alternative hypothesis. 7. A random variable X has the following probability distribution: X: 0 1 2 3 4 5 6 7 8 P(X): 5a 7a 9a 11a 13a 15a 17a. Find the value of a.
Understand the Problem
The question involves various problems related to probability, statistics, and hypothesis testing. Each item asks for calculations or explanations based on given parameters or distributions, such as drawing balls from a bag, determining probabilities after rolling a dice, handling a Poisson distribution, and hypothesis testing.
Answer
With replacement: $P = \frac{63}{128}$; Without replacement: $P = \frac{21}{80}$.
Answer for screen readers
The total probability of drawing one white and one black ball with replacement is:
$$ P(\text{with replacement}) = 2 \times \left(\frac{7}{16} \times \frac{9}{16}\right) = \frac{126}{256} = \frac{63}{128} $$
The total probability of drawing one white and one black ball without replacement is:
$$ P(\text{without replacement}) = \left(\frac{7}{16} \times \frac{9}{15}\right) + \left(\frac{9}{16} \times \frac{7}{15}\right) = \frac{63}{240} = \frac{21}{80} $$
Steps to Solve
-
Determine the total number of balls The total number of balls in the bag is given by adding the white and black balls:
$$ 7 + 9 = 16 $$ -
Calculate the probability of drawing one white and one black ball with replacement If the balls are replaced, the probability of drawing a white ball first and then a black ball is:
$$ P(WB) = P(W) \times P(B) = \left(\frac{7}{16}\right) \times \left(\frac{9}{16}\right) $$
Similarly, the probability of drawing a black ball first and then a white ball is:
$$ P(BW) = P(B) \times P(W) = \left(\frac{9}{16}\right) \times \left(\frac{7}{16}\right) $$
Thus, the total probability is: $$ P(WB) + P(BW) = 2 \times \left(\frac{7}{16} \times \frac{9}{16}\right) $$ -
Calculate the probability of drawing one white and one black ball without replacement If the balls are not replaced, the probability of drawing a white ball first and then a black ball is:
$$ P(WB) = P(W) \times P(B|W) = \left(\frac{7}{16}\right) \times \left(\frac{9}{15}\right) $$
The probability of drawing a black ball first and then a white ball is:
$$ P(BW) = P(B) \times P(W|B) = \left(\frac{9}{16}\right) \times \left(\frac{7}{15}\right) $$
The total probability is then: $$ P(WB) + P(BW) = \left(\frac{7}{16} \times \frac{9}{15}\right) + \left(\frac{9}{16} \times \frac{7}{15}\right) $$
The total probability of drawing one white and one black ball with replacement is:
$$ P(\text{with replacement}) = 2 \times \left(\frac{7}{16} \times \frac{9}{16}\right) = \frac{126}{256} = \frac{63}{128} $$
The total probability of drawing one white and one black ball without replacement is:
$$ P(\text{without replacement}) = \left(\frac{7}{16} \times \frac{9}{15}\right) + \left(\frac{9}{16} \times \frac{7}{15}\right) = \frac{63}{240} = \frac{21}{80} $$
More Information
The probabilities calculated here are examples of how to apply the multiplication rule in probability theory. Drawing balls and replacement concept illustrate fundamental principles in probability concerning dependent and independent events.
Tips
- Confusing Replacement and Non-Replacement: Forgetting to adjust probabilities when not replacing the drawn ball can lead to incorrect answers.
- Miscalculating Total Possibilities: Ensure that total outcomes are correctly counted when calculating probabilities.
AI-generated content may contain errors. Please verify critical information