∫(1 + 3x)x² dx
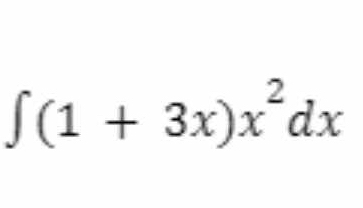
Understand the Problem
The question asks to find the integral of the expression (1 + 3x)x² with respect to x. The solution will involve applying integration techniques such as polynomial expansion and power rule for integration.
Answer
$$ \frac{x^3}{3} + \frac{3x^4}{4} + C $$
Answer for screen readers
The integral of the expression is
$$ \frac{x^3}{3} + \frac{3x^4}{4} + C $$
Steps to Solve
- Expand the Expression
First, we need to expand the expression ( (1 + 3x)x^2 ).
[ (1 + 3x)x^2 = x^2 + 3x^3 ]
- Set Up the Integral
Now, set up the integral with the expanded expression:
[ \int (x^2 + 3x^3) , dx ]
- Apply the Power Rule
Use the power rule of integration, which states that
[ \int x^n , dx = \frac{x^{n+1}}{n+1} + C ]
to integrate each term:
- For ( x^2 ):
[ \int x^2 , dx = \frac{x^{2 + 1}}{2 + 1} = \frac{x^3}{3} ]
- For ( 3x^3 ):
[ \int 3x^3 , dx = 3 \cdot \frac{x^{3 + 1}}{3 + 1} = \frac{3x^4}{4} ]
- Combine the Results
Combining the results from the integration:
[ \int (x^2 + 3x^3) , dx = \frac{x^3}{3} + \frac{3x^4}{4} + C ]
The integral of the expression is
$$ \frac{x^3}{3} + \frac{3x^4}{4} + C $$
More Information
This result represents the antiderivative of the original expression. The constant ( C ) accounts for the family of functions that share the same derivative.
Tips
- Forgetting to distribute correctly when expanding ( (1 + 3x)x^2 ).
- Misapplying the power rule, especially with the constants.
- Omitting the constant ( C ) in the final answer.
AI-generated content may contain errors. Please verify critical information