( 1 1 ) ( x1 ) = ( 3 ) ( -1 1 ) ( x2 ) ( 1 )
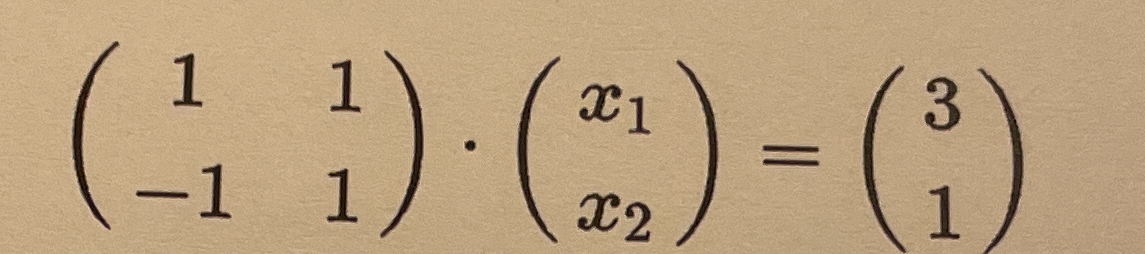
Understand the Problem
The question represents a matrix equation that involves multiplying a 2x2 matrix with a 2x1 vector, resulting in another 2x1 vector. The task is to find the values of x1 and x2 that satisfy the equation.
Answer
The values are \(x_1 = 1\) and \(x_2 = 2\).
Answer for screen readers
The values are (x_1 = 1) and (x_2 = 2).
Steps to Solve
- Set Up the Matrix Equation We have the matrix equation:
$$ \begin{pmatrix} 1 & 1 \ -1 & 1 \end{pmatrix} \begin{pmatrix} x_1 \ x_2 \end{pmatrix}
\begin{pmatrix} 3 \ 1 \end{pmatrix} $$
-
Write the System of Equations From the matrix multiplication, we can derive the following system of equations:
-
(1 \cdot x_1 + 1 \cdot x_2 = 3)
-
(-1 \cdot x_1 + 1 \cdot x_2 = 1)
This simplifies to:
-
(x_1 + x_2 = 3 \quad \text{(Equation 1)})
-
(-x_1 + x_2 = 1 \quad \text{(Equation 2)})
-
Express (x_2) in Terms of (x_1) From Equation 1, we can express (x_2) as:
$$ x_2 = 3 - x_1 $$
- Substitute (x_2) into Equation 2 Substitute (x_2) into Equation 2:
$$ -x_1 + (3 - x_1) = 1 $$
- Simplify and Solve for (x_1) Combine like terms:
$$ -2x_1 + 3 = 1 $$
Subtract 3 from both sides:
$$ -2x_1 = -2 $$
Divide by -2:
$$ x_1 = 1 $$
- Find (x_2) Now substitute (x_1) back into the equation for (x_2):
$$ x_2 = 3 - 1 = 2 $$
The values are (x_1 = 1) and (x_2 = 2).
More Information
This type of problem involves solving a system of linear equations, which occur frequently in linear algebra and can represent various real-world problems, such as optimization and resource allocation.
Tips
- Forgetting to distribute the negative sign in the second equation can lead to an incorrect solution.
- Misreading the resultant vector (confusing the values placed in the matrix).
AI-generated content may contain errors. Please verify critical information