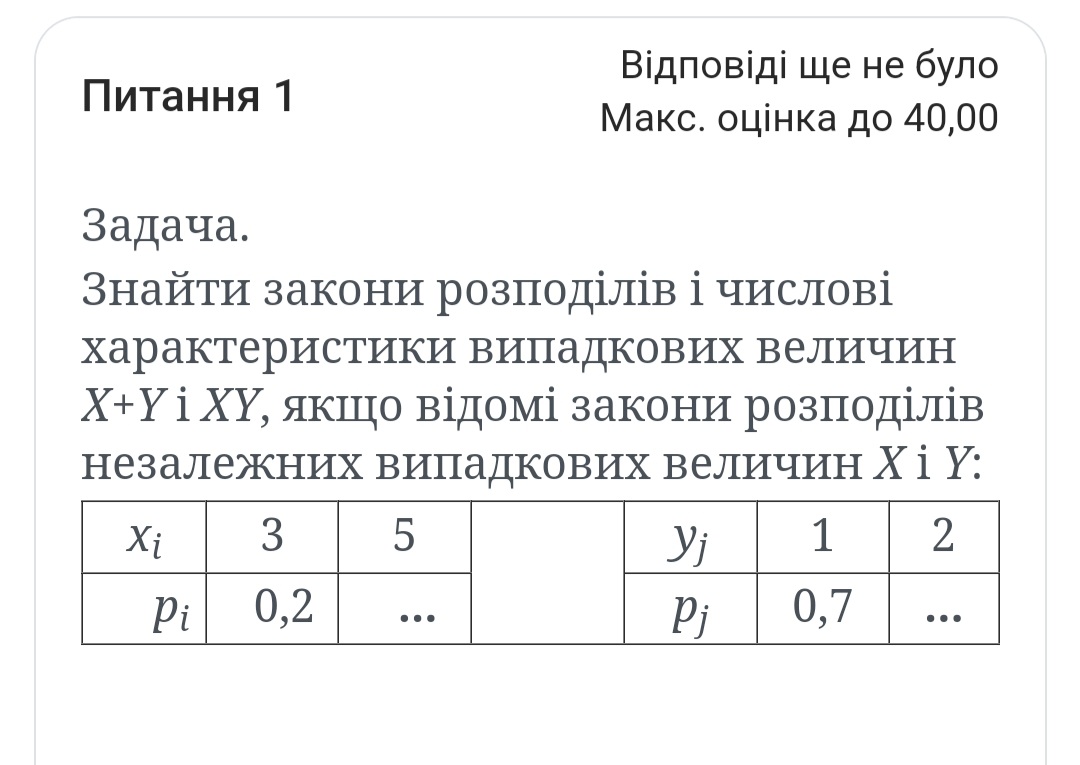
Знайти закони розподілів і числові характеристики випадкових величин X+Y і XY, якщо відомі закони розподілів незалежних випадкових величин X і Y. Знайти закони розподілів і числові характеристики випадкових величин X+Y і XY, якщо відомі закони розподілів незалежних випадкових величин X і Y.
Understand the Problem
Запит стосується статистичної задачі, де потрібно знайти закони розподілів і числові характеристики сум випадкових величин X+Y та добутку XY, якщо відомі розподіли незалежних випадкових величин X і Y.
Answer
Розподіл $X + Y$: $P(X+Y=4)=0.14$, $P(X+Y=5)=0.06$, $P(X+Y=6)=0.56$, $P(X+Y=7)=0.24$; Розподіл $XY$: $P(XY=3)=0.14$, $P(XY=5)=0.56$, $P(XY=6)=0.06$, $P(XY=10)=0.24$.
Answer for screen readers
Розподіл $X + Y$:
- $4$: $0.14$
- $5$: $0.06$
- $6$: $0.56$
- $7$: $0.24$
Розподіл $XY$:
- $3$: $0.14$
- $5$: $0.56$
- $6$: $0.06$
- $10$: $0.24$
Steps to Solve
- Знайдемо розподіли X і Y
Дано розподіл випадкової величини $X$ з $p_X(3) = 0.2$ та $p_X(5) = p_X(3) + 0.8 = 0.8$ (оскільки ймовірності повинні складати 1).
Для випадкової величини $Y$ маємо: $p_Y(1) = 0.7$ та $p_Y(2) = 0.3$ (оскільки ймовірності повинні складати 1).
- Розподіл суми X + Y
Щоб знайти розподіл суми $X + Y$, потрібно усі можливі комбінації $X$ та $Y$ скласти:
-
Для $X=3$:
- $Y=1 \Rightarrow X + Y = 4$, ймовірність $= 0.2 \cdot 0.7 = 0.14$
- $Y=2 \Rightarrow X + Y = 5$, ймовірність $= 0.2 \cdot 0.3 = 0.06$
-
Для $X=5$:
- $Y=1 \Rightarrow X + Y = 6$, ймовірність $= 0.8 \cdot 0.7 = 0.56$
- $Y=2 \Rightarrow X + Y = 7$, ймовірність $= 0.8 \cdot 0.3 = 0.24$
Отже, підсумовуючи:
- $X + Y = 4 \to P = 0.14$
- $X + Y = 5 \to P = 0.06$
- $X + Y = 6 \to P = 0.56$
- $X + Y = 7 \to P = 0.24$
- Розподіл добутку XY
Для обчислення розподілу добутку $XY$:
-
Для $X = 3$:
- $Y = 1 \Rightarrow XY = 3$, ймовірність $= 0.2 \cdot 0.7 = 0.14$
- $Y = 2 \Rightarrow XY = 6$, ймовірність $= 0.2 \cdot 0.3 = 0.06$
-
Для $X = 5$:
- $Y = 1 \Rightarrow XY = 5$, ймовірність $= 0.8 \cdot 0.7 = 0.56$
- $Y = 2 \Rightarrow XY = 10$, ймовірність $= 0.8 \cdot 0.3 = 0.24$
Отже, підсумовуючи:
- $XY = 3 \to P = 0.14$
- $XY = 5 \to P = 0.56$
- $XY = 6 \to P = 0.06$
- $XY = 10 \to P = 0.24$
Розподіл $X + Y$:
- $4$: $0.14$
- $5$: $0.06$
- $6$: $0.56$
- $7$: $0.24$
Розподіл $XY$:
- $3$: $0.14$
- $5$: $0.56$
- $6$: $0.06$
- $10$: $0.24$
More Information
Ці розподіли допомагають зрозуміти, як взаємодіють незалежні випадкові величини. Закон розподілу допомагає в статистичному аналізі та інших галузях, де важливо знати, які можуть бути результати комбінацій величин.
Tips
- Помилково підрахування ймовірностей при комбінаціях $X$ і $Y$.
- Неувага до того, що ймовірності кожної комбінації мають бути правильно підраховані.
AI-generated content may contain errors. Please verify critical information