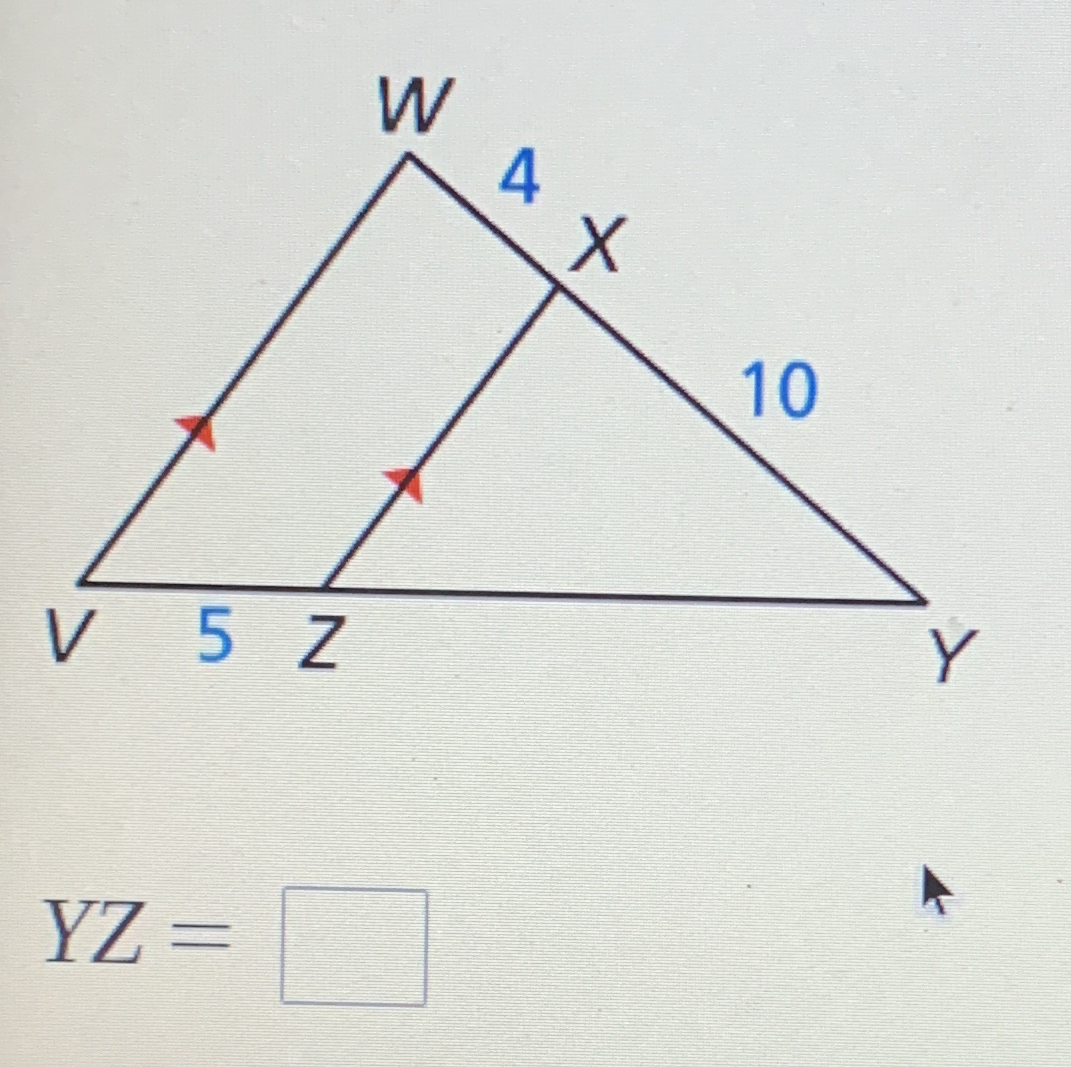
YZ = ?
Understand the Problem
The question is asking to find the length of segment YZ in the given triangle, using the dimensions and the properties of the triangle.
Answer
The length of segment $YZ$ is $8$.
Answer for screen readers
The length of segment $YZ$ is $8$.
Steps to Solve
- Identify the Given Values We know the lengths of sides and the segment lengths:
- $VW = 5$
- $WY = 10$
- $WX = 4$
-
Use the Triangle Proportions Since triangle $VWZ$ is similar to triangle $WXY$, we can set up a proportion based on their corresponding sides: $$ \frac{VW}{WY} = \frac{XZ}{YZ} $$ This gives us: $$ \frac{5}{10} = \frac{4}{YZ} $$
-
Solve for $YZ$ Cross-multiplying gives: $$ 5 \cdot YZ = 10 \cdot 4 $$ Hence: $$ 5 \cdot YZ = 40 $$ To isolate $YZ$, divide both sides by 5: $$ YZ = \frac{40}{5} $$
-
Calculate the Final Length of $YZ$ Perform the division: $$ YZ = 8 $$
The length of segment $YZ$ is $8$.
More Information
In similar triangles, the ratio of the lengths of corresponding sides remains constant. This allows us to solve for unknown lengths when two triangles are similar.
Tips
- Confusing the corresponding sides of the similar triangles can lead to incorrect proportions.
- Forgetting to cross-multiply properly.
AI-generated content may contain errors. Please verify critical information