यदि A=[2+10] [3] B=[1-i] [2i] A + B का मान बताओ-1
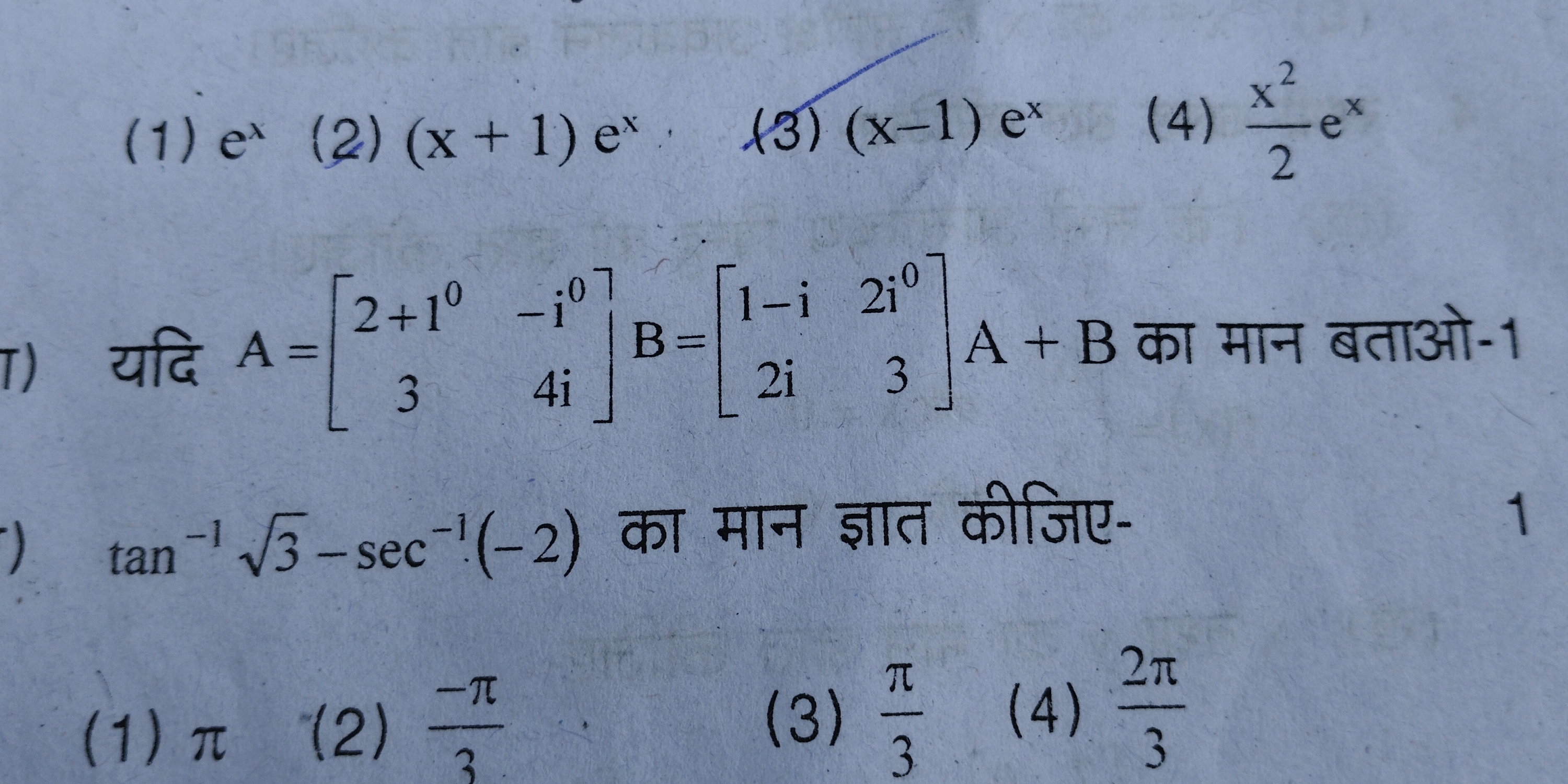
Understand the Problem
यह प्रश्न A और B नामक दो मैट्रिक्सों के योग और उनके मान की गणना करने के लिए है। मैट्रिक्स A और B के दिए गए मान के आधार पर, हम परिकलित करेंगे कि A + B का मान कितना है।
Answer
$$ A + B = \begin{bmatrix} 13 - i \end{bmatrix} $$
Answer for screen readers
$$ A + B = \begin{bmatrix} 13 - i \end{bmatrix} $$
Steps to Solve
-
Calculate Values of A and B
Given matrices:
$$ A = \begin{bmatrix} 2 + 10 \end{bmatrix} = \begin{bmatrix} 12 \end{bmatrix} $$
$$ B = \begin{bmatrix} 1 - i \end{bmatrix} $$
-
Add the Matrices
Now, we add matrices A and B:
$$ A + B = \begin{bmatrix} 12 \end{bmatrix} + \begin{bmatrix} 1 - i \end{bmatrix} $$
This results in:
$$ A + B = \begin{bmatrix} 12 + (1 - i) \end{bmatrix} = \begin{bmatrix} 12 + 1 - i \end{bmatrix} = \begin{bmatrix} 13 - i \end{bmatrix} $$
-
Final Result
The value of $ A + B $ is:
$$ A + B = \begin{bmatrix} 13 - i \end{bmatrix} $$
$$ A + B = \begin{bmatrix} 13 - i \end{bmatrix} $$
More Information
The result ( 13 - i ) represents a complex number where 13 is the real part and (-i) is the imaginary part.
Tips
- Confusing the addition of complex numbers: Always remember to add the real parts and the imaginary parts separately.
- Forgetting parentheses when dealing with complex numbers.
AI-generated content may contain errors. Please verify critical information