यदि 5 + 2√3 / 7 + 4√3 = a + b√3 है, तो a और b का मान ज्ञात कीजिए।
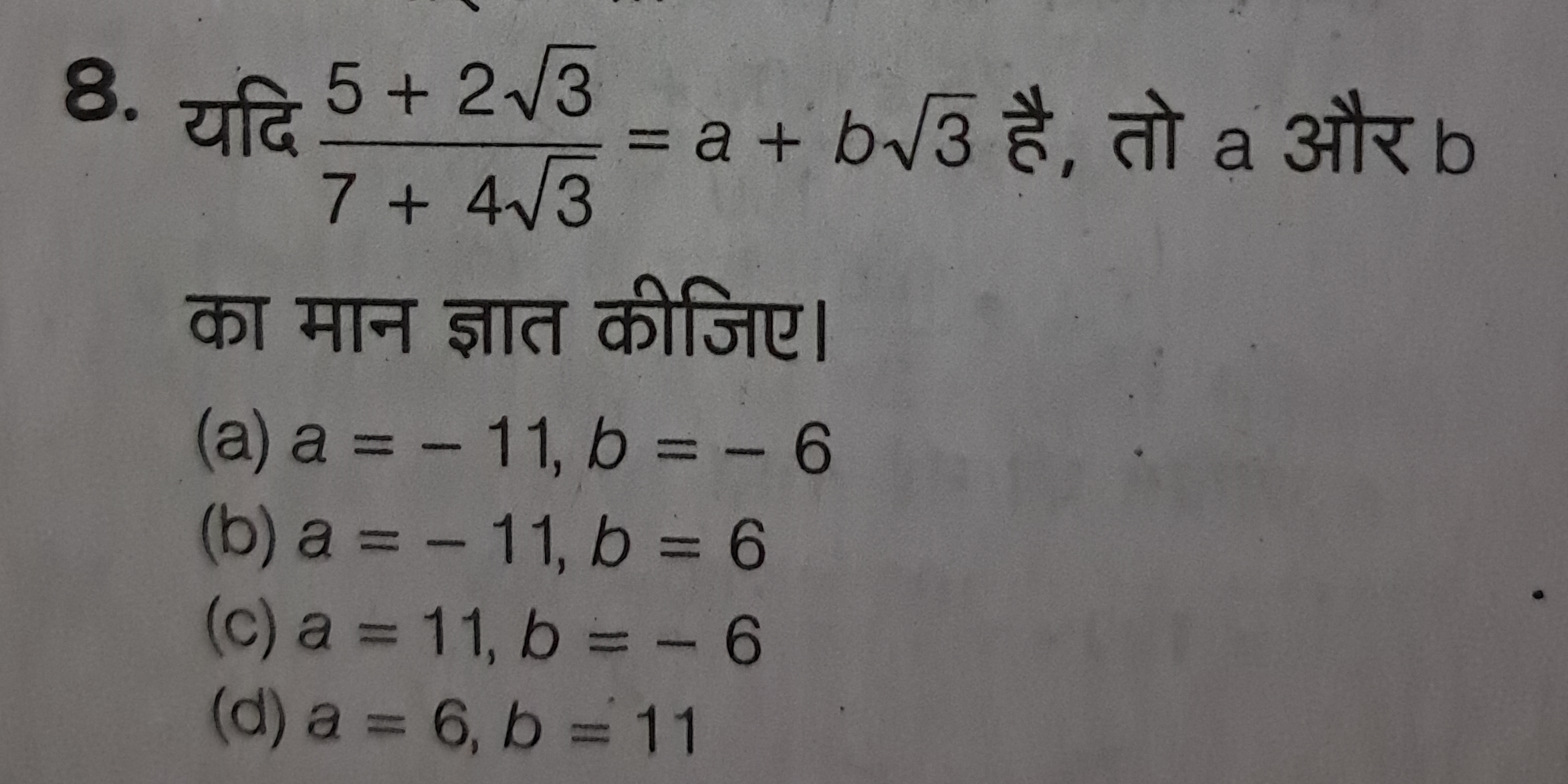
Understand the Problem
यह प्रश्न एक समीकरण की तुलना कर रहा है जिसमें 5 + (2√3)/(7 + 4√3) = a + b√3 है। इस समीकरण के लिए a और b के मान ज्ञात करने की आवश्यकता है।
Answer
$a = 11, b = -6$
Answer for screen readers
$a = 11, b = -6$
Steps to Solve
- समीकरण को सरल करना
हम समीकरण को निम्नलिखित रूप में लिख सकते हैं: $$ \frac{5 + 2\sqrt{3}}{7 + 4\sqrt{3}} $$
- गुणनफल करके परिणाम को प्राप्त करना
इस समीकरण को सरल करने के लिए, हम भुजाओं को साझा करते हैं। इसलिए, हम बहुपद को गुणा करेंगे: $$ = \frac{(5 + 2\sqrt{3})(7 - 4\sqrt{3})}{(7 + 4\sqrt{3})(7 - 4\sqrt{3})} $$
- अंक प्राप्त करना
अब हम अंक को प्राप्त करेंगे। अंश: $$ = (5 \times 7) + (5 \times -4\sqrt{3}) + (2\sqrt{3} \times 7) + (2\sqrt{3} \times -4\sqrt{3}) $$ यह हमें: $$ = 35 - 20\sqrt{3} + 14\sqrt{3} - 24 $$ $$ = 11 - 6\sqrt{3} $$
- हर भाग को सरल बनाना
अब हर भाग को सरल करते हैं। हर भाग को घटाते हैं: $$ = \frac{11 - 6\sqrt{3}}{(49 - 48)} $$ $$ = 11 - 6\sqrt{3} $$
- a और b का मान निकालना
हम देख सकते हैं कि: $$ a = 11, b = -6 $$
$a = 11, b = -6$
More Information
यह समाधान समीकरण के दोनों भागों की तुलना कर के $a$ और $b$ के मान को निकालने के लिए किया गया है। समीकरण की उचित समझ से हमें सरलता से इन मानों को प्राप्त करने में मदद मिली।
Tips
- समीकरण को गुणा करते समय सटीकता न होना।
- अंश और हर को गलत सरल करना।
- सकारात्मक और नकारात्मक चिह्नों को गलत तरीके से समझना।
AI-generated content may contain errors. Please verify critical information