∫ x^(2/3)√x dx
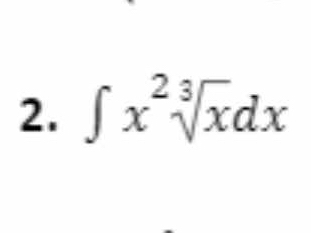
Understand the Problem
The question is asking for the evaluation of the integral of the function x raised to the power of 2/3 multiplied by the square root of x, which requires integration techniques.
Answer
$$ \frac{6}{13} x^{13/6} + C $$
Answer for screen readers
The final answer is:
$$ \frac{6}{13} x^{13/6} + C $$
Steps to Solve
- Rewrite the integrand
The integrand can be simplified. Since $\text{√} , x = x^{1/2}$, we can rewrite the integral:
$$ \int x^{2/3} \sqrt{x} , dx = \int x^{2/3} \cdot x^{1/2} , dx $$
- Combine the exponents
Using the property of exponents, $a^m \cdot a^n = a^{m+n}$, we can combine the terms:
$$ = \int x^{2/3 + 1/2} , dx $$
- Calculate the combined exponent
To combine $2/3$ and $1/2$, we need a common denominator:
- The common denominator of 3 and 2 is 6.
- Convert $2/3$ to $4/6$ and $1/2$ to $3/6$.
- Thus, $2/3 + 1/2 = \frac{4}{6}+\frac{3}{6}=\frac{7}{6}$.
So the integral now becomes:
$$ = \int x^{7/6} , dx $$
- Integrate the function
We apply the power rule of integration, which states $\int x^n , dx = \frac{x^{n+1}}{n+1} + C$, where $C$ is the constant of integration.
Here, we have $n = 7/6$:
$$ = \frac{x^{7/6 + 1}}{7/6 + 1} + C $$
- Calculate the new exponent and simplify
The new exponent is:
$$ 7/6 + 1 = 7/6 + 6/6 = 13/6 $$
Thus, we can write the integral as:
$$ = \frac{x^{13/6}}{13/6} + C $$
To simplify further:
$$ = \frac{6}{13} x^{13/6} + C $$
The final answer is:
$$ \frac{6}{13} x^{13/6} + C $$
More Information
This integral represents the area under the curve of the function $x^{2/3} \sqrt{x}$ over a given interval. The power rule of integration simplifies the process, allowing us to work with exponents instead of relying on more complex techniques.
Tips
- Incorrect exponent addition: Make sure to find a common denominator when adding fractions.
- Neglecting the constant of integration: Always remember to include the constant $C$ in indefinite integrals.
AI-generated content may contain errors. Please verify critical information