x^2 dy/dx + y^2 = x*y

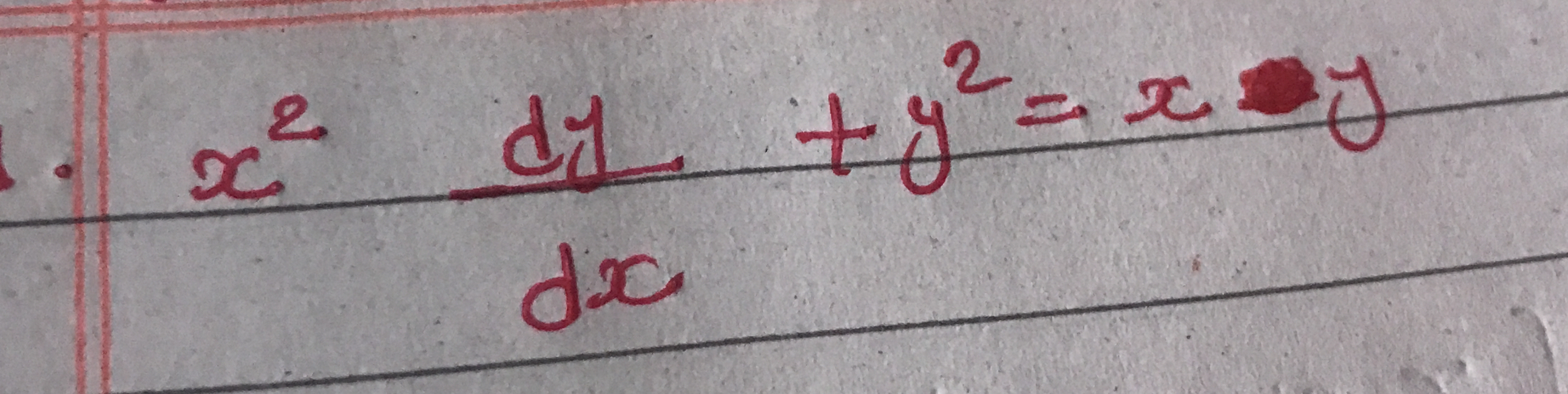
Understand the Problem

The question appears to present a differential equation involving both x and y variables, and it asks for a solution or further manipulation of this equation. The equation shown involves derivatives and algebraic terms, which suggests a calculus problem related to differential equations.

Answer

The general solution is given by: $$ \ln |y| - \frac{y}{x} = -\frac{1}{x} + C $$

Steps to Solve

Rearranging the Differential Equation

Start with the original equation: $$ x^2 \frac{dy}{dx} + y^2 = xy $$ Rearranging gives: $$ x^2 \frac{dy}{dx} = xy - y^2 $$

Dividing by (x^2)

Next, divide every term by (x^2) to isolate the derivative: $$ \frac{dy}{dx} = \frac{xy - y^2}{x^2} $$

Separating Variables

Separate the variables (y) and (x): $$ \frac{dy}{xy - y^2} = \frac{dx}{x^2} $$

Integrating Both Sides

Now we will integrate both sides:

Left side integration: $$ \int \frac{dy}{y(x - y)} $$
Right side integration: $$ \int \frac{dx}{x^2} $$

Integrating the Left Side

Use partial fraction decomposition: $$ \frac{1}{y(x-y)} = \frac{A}{y} + \frac{B}{x-y} $$ Finding constants (A) and (B), we rewrite and simplify, then we can integrate.

Integrating the Right Side

The integral of the right side results in: $$ -\frac{1}{x} + C $$

Combining Results

Combine the results from both integrals to get the general solution.

The general solution to the differential equation is: $$ \ln |y| - \frac{y}{x} = -\frac{1}{x} + C $$

More Information

The solution represents a family of curves that satisfy the original differential equation. Understanding differential equations is vital for modeling real-world scenarios in physics and engineering.

Tips

Forgetting to properly separate the variables.
Miscalculating during integration, especially with partial fractions.
Not applying the constant of integration clearly.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!