∫ (x² + 4x³ + 2) / (6x) dx
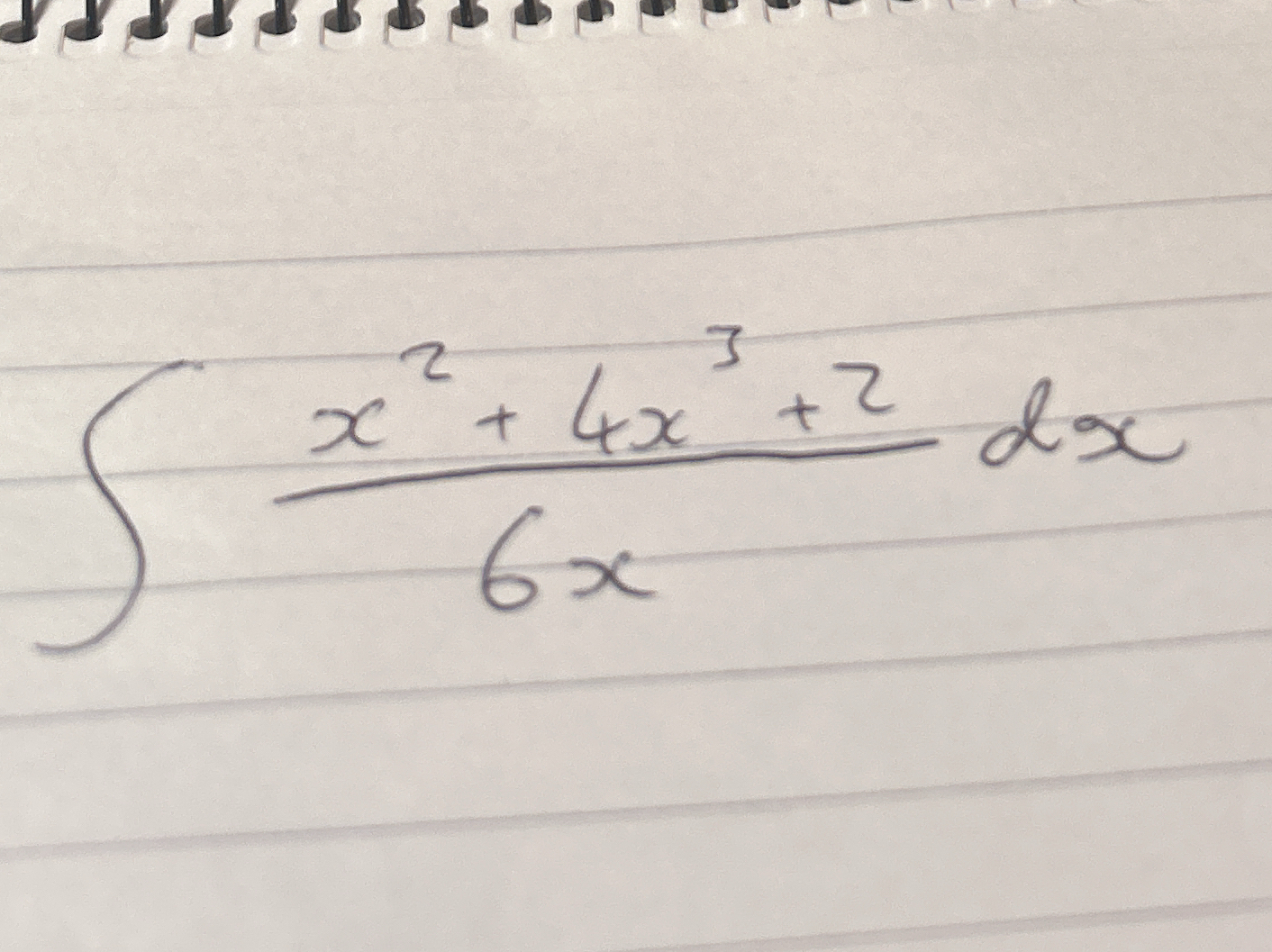
Understand the Problem
The question involves calculating the integral of the function (x² + 4x³ + 2) / (6x) with respect to x. This requires applying integration techniques.
Answer
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
Answer for screen readers
The integral is: $$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
Steps to Solve
- Simplify the integrand
Start by simplifying the expression ( \frac{x^2 + 4x^3 + 2}{6x} ). Divide each term in the numerator by ( 6x ): [ \frac{x^2}{6x} + \frac{4x^3}{6x} + \frac{2}{6x} = \frac{x}{6} + \frac{2}{3}x^2 + \frac{1}{3x} ]
- Set up the integral
Now, rewrite the integral: [ \int \left( \frac{x}{6} + \frac{2}{3}x^2 + \frac{1}{3x} \right) , dx ]
- Integrate each term
Integrate each term separately: [ \int \frac{x}{6} , dx = \frac{1}{6} \cdot \frac{x^2}{2} = \frac{x^2}{12} ] [ \int \frac{2}{3}x^2 , dx = \frac{2}{3} \cdot \frac{x^3}{3} = \frac{2x^3}{9} ] [ \int \frac{1}{3x} , dx = \frac{1}{3} \ln |x| ]
- Combine the results
Now combine the results of the integrals: [ \int \frac{x^2 + 4x^3 + 2}{6x} , dx = \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C ]
- Final Form
Thus, the final form of the integral is: [ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C ]
The integral is: $$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{1}{3} \ln |x| + C $$
More Information
This integral combines polynomial and logarithmic integration techniques. The constant ( C ) represents the constant of integration, which can vary depending on the context.
Tips
- Confusing the integration of different types of functions, particularly logarithmic versus polynomial.
- Forgetting to include the constant of integration ( C ).
