∫ (x^2 + 4x^3 + 2) / (6x) dx
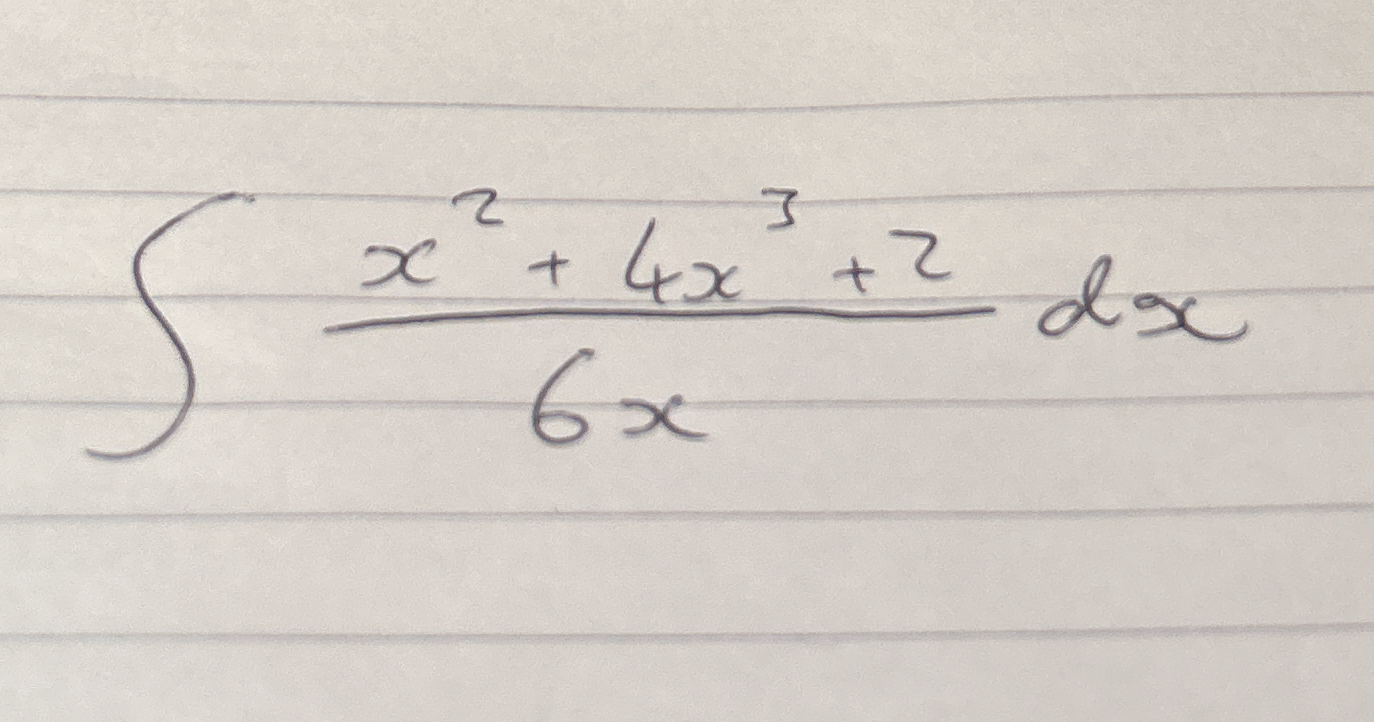
Understand the Problem
The question is asking for the integral of a rational function, specifically the integral of (x^2 + 4x^3 + 2) divided by (6x) with respect to x. This involves simplifying the expression before integrating it.
Answer
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{\ln |x|}{3} + C $$
Answer for screen readers
The final answer is:
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{\ln |x|}{3} + C $$
Steps to Solve
- Simplify the Rational Function First, we can simplify the expression inside the integral:
$$ \frac{x^2 + 4x^3 + 2}{6x} = \frac{1}{6} \left( \frac{x^2}{x} + \frac{4x^3}{x} + \frac{2}{x} \right) $$
This gives us:
$$ \frac{1}{6} \left( x + 4x^2 + \frac{2}{x} \right) $$
- Rewrite the Integral Now we can rewrite the integral using our simplified expression:
$$ \int \frac{x^2 + 4x^3 + 2}{6x} , dx = \frac{1}{6} \int \left( x + 4x^2 + \frac{2}{x} \right) dx $$
- Integrate Each Term Now, we will integrate each term individually:
- For the first term, $x$, the integral is:
$$ \int x , dx = \frac{x^2}{2} $$
- For the second term, $4x^2$, the integral is:
$$ \int 4x^2 , dx = \frac{4x^3}{3} $$
- For the third term, $\frac{2}{x}$, the integral is:
$$ \int \frac{2}{x} , dx = 2 \ln |x| $$
Putting this all together:
$$ \int \left( x + 4x^2 + \frac{2}{x} \right) dx = \frac{x^2}{2} + \frac{4x^3}{3} + 2 \ln |x| $$
- Combine and Scale the Result We multiply the entire integral by $\frac{1}{6}$:
$$ \frac{1}{6} \left( \frac{x^2}{2} + \frac{4x^3}{3} + 2 \ln |x| \right) = \frac{x^2}{12} + \frac{2x^3}{9} + \frac{\ln |x|}{3} + C $$
where $C$ is the constant of integration.
The final answer is:
$$ \frac{x^2}{12} + \frac{2x^3}{9} + \frac{\ln |x|}{3} + C $$
More Information
This integral combines polynomial and logarithmic functions. It's often useful to simplify rational expressions before integrating. The integration of basic polynomial terms is straightforward and follows the power rule.
Tips
- Forgetting to simplify the rational expression before integrating can lead to complex calculations.
- Skipping the constant of integration ($C$) at the end of the integral.
AI-generated content may contain errors. Please verify critical information